题目内容
12.设复数z满足z2=3+4i(i为虚数单位),则z的虚部为±1,|z|=$\sqrt{5}$.分析 由复数的定义即可求出,直接利用复数的模的求解法则,化简求解即可.
解答 解:z2=3+4i=(2+i)2=(-2-i)2,
∴z=2+i,或z=-2-i,
∴则z的虚部为±1,
复数z满足z2=3+4i,
可得|z||z|=|3+4i|=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴|z|=$\sqrt{5}$
故答案为:$±1,\sqrt{5}$
点评 本题考查复数的模以及复数的定义,注意复数的模的运算法则的应用,考查计算能力.

练习册系列答案
相关题目
20.下列函数既是奇函数又在区间(0,+∞)上为增函数的是( )
| A. | y=sinx,x∈R | B. | y=x2,x∈R | C. | y=x-$\frac{1}{x}$,x≠0 | D. | y=2-x,x∈R |
1.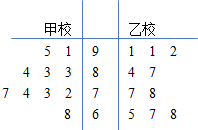 为了解高一新生数学基础,甲、乙两校对高一新生进行了数学测试.现从两校各随机抽取10名新生的成绩作为样本,他们的测试成绩的茎叶图如下:
为了解高一新生数学基础,甲、乙两校对高一新生进行了数学测试.现从两校各随机抽取10名新生的成绩作为样本,他们的测试成绩的茎叶图如下:
(1)比较甲、乙两校新生的数学测试样本成绩的平均值及方差的大小;(只需要写出结论)
(2)如果将数学基础采用A、B、C等级制,各等级对应的测试成绩标准如表:(满分100分,所有学生成绩均在60分以上)
假设每个新生的测试成绩互相独立.根据所给数据,以事件发生的频率作为相应事件发生的概率.
从甲、乙两校新生中各随机抽取一名新生,求甲校新生的数学基础等级高于乙校新生的数学基础等级的概率.
 为了解高一新生数学基础,甲、乙两校对高一新生进行了数学测试.现从两校各随机抽取10名新生的成绩作为样本,他们的测试成绩的茎叶图如下:
为了解高一新生数学基础,甲、乙两校对高一新生进行了数学测试.现从两校各随机抽取10名新生的成绩作为样本,他们的测试成绩的茎叶图如下:(1)比较甲、乙两校新生的数学测试样本成绩的平均值及方差的大小;(只需要写出结论)
(2)如果将数学基础采用A、B、C等级制,各等级对应的测试成绩标准如表:(满分100分,所有学生成绩均在60分以上)
| 测试成绩 | [85,100] | [70,85) | (60,70) |
| 基础等级 | A | B | C |
从甲、乙两校新生中各随机抽取一名新生,求甲校新生的数学基础等级高于乙校新生的数学基础等级的概率.
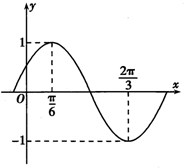 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.