题目内容
12．（1-x）6（1+x）4的展开式中x2的系数是（ ）| A． | -4 | B． | -3 | C． | 3 | D． | 4 |
分析 把已知二项式变形，然后展开二项式定理，则展开式中x2的系数可求．
解答 解：（1-x）6（1+x）4 =（1-2x+x2）（1-x2）4
=（1-2x+x2）$（{C}_{4}^{0}-{C}_{4}^{1}{x}^{2}+{C}_{4}^{2}{x}^{4}-{C}_{4}^{3}{x}^{6}+{C}_{4}^{4}{x}^{8}）$．
∴（1-x）6（1+x）4的展开式中x2的系数是${C}_{4}^{0}-{C}_{4}^{1}=-3$．
故选：B．
点评 本题考查二项式系数的性质，关键是熟记二项展开式的通项，是基础题．
练习册系列答案
相关题目
20．
在一次文、理科学习倾向的调研中，对高一年段1000名学生进行文综、理综各一次测试（满分均为300分）．测试后，随机抽取若干名学生成绩，记理综成绩X，文综成绩为Y，|X-Y|为Z，将Z值分组统计制成下表，并将其中女生的Z值分布情况制成频率分布直方图
值分布情况制成频率分布直方图（如图所示）．
（Ⅰ）若已知直方图中[60，80）频数为25，试分别估计全体学生中，Z∈[0，20）的男、女生人数；
（Ⅱ）记Z的平均数为$\overline{Z}$，如果$\overline{Z}$＞60称为整体具有学科学习倾向，试估计高一年段女生的$\overline{Z}$值（同一组中的数据用该组区间中点值作代表），并判断高一年段女生是否整体具有显著学科学习倾向．
在一次文、理科学习倾向的调研中，对高一年段1000名学生进行文综、理综各一次测试（满分均为300分）．测试后，随机抽取若干名学生成绩，记理综成绩X，文综成绩为Y，|X-Y|为Z，将Z值分组统计制成下表，并将其中女生的Z值分布情况制成频率分布直方图值分布情况制成频率分布直方图（如图所示）．
| 分组 | [0，20） | [20，40） | [40，60} | [60，80） | [80，100） | [100，120） | [120，140） |
| 频数 | 4 | 18 | 42 | 66 | 48 | 20 | 2 |
（Ⅱ）记Z的平均数为$\overline{Z}$，如果$\overline{Z}$＞60称为整体具有学科学习倾向，试估计高一年段女生的$\overline{Z}$值（同一组中的数据用该组区间中点值作代表），并判断高一年段女生是否整体具有显著学科学习倾向．
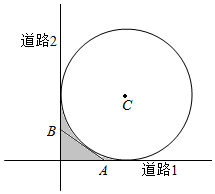如图，某城市有一块半径为1（单位：百米）的圆形景观，圆心为C，有两条与圆形景观相切且互相垂直的道路．最初规划在拐角处（图中阴影部分）只有一块绿化地，后来有众多市民建议在绿化地上建一条小路，便于市民快捷地往返两条道路．规划部门采纳了此建议，决定在绿化地中增建一条与圆C相切的小道AB．问：A，B两点应选在何处可使得小道AB最短？
1．已知集合A={x||x|＜1}，B={x|x2-x≤0}，则A∩B=（ ）
| A． | {x|-1≤x≤1} | B． | {x|0≤x≤1} | C． | {x|0＜x≤1} | D． | {x|0≤x＜1} |