题目内容
13.设函数f(x)=|x+1|-|2x-a|(Ⅰ)当a=2,解不等式f(x)<0
(Ⅱ)若a>0,且对于任意的实数x,都有f(x)≤3,求a的取值范围.
分析 (Ⅰ)将a=2代入,不等式两边平方,解出即可;(Ⅱ)通过讨论x的范围,得到f(x)的分段函数,求出f(x)的最大值,从而求出a的范围即可.
解答 解:(Ⅰ)a=2时,原不等式为:|x+1|-|2x-2|<0,
即|x+1|<|2x-2|,平方:(x+1)2<(2x-2)2,
化简得:(3x-1)(x-3)>0,解得:x<$\frac{1}{3}$或x>3,
故解集为:{x|x<$\frac{1}{3}$或x>3};
(Ⅱ)∵a>0,∴$\frac{a}{2}$>0,
∴原函数可化为:
f(x)=$\left\{\begin{array}{l}{-(x+1)+(2x-a),x≤-1}\\{(x+1)+(2x-a),-1<x≤\frac{a}{2}}\\{(x+1)-(2x-a),x>\frac{a}{2}}\end{array}\right.$,
即f(x)=$\left\{\begin{array}{l}{x-1-a,x≤-1}\\{3x+1-a,-1<x≤\frac{a}{2}}\\{-x+1+a,x>\frac{a}{2}}\end{array}\right.$,
∴f(x)max=f($\frac{a}{2}$)=$\frac{a}{2}$+1,
∴$\frac{a}{2}$+1≤3,解得:a≤4,
综上,a的范围是(0,4].
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
1.已知集合A={x||x|<1},B={x|x2-x≤0},则A∩B=( )
| A. | {x|-1≤x≤1} | B. | {x|0≤x≤1} | C. | {x|0<x≤1} | D. | {x|0≤x<1} |
18.已知集合A={x||x-1|≤1,x∈R},${B}=\left\{{x\left|{\sqrt{x}≤2,x∈{Z}}\right.}\right\}$,则A∩B=( )
| A. | (0,2) | B. | [0,2] | C. | {0,2} | D. | {0,1,2} |
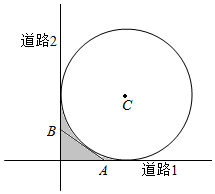 如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?
如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?