题目内容
在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c=
,4cos2
-cos2C=
.
(1)求角C的大小;
(2)求△ABC的面积.
| 7 |
| C |
| 2 |
| 7 |
| 2 |
(1)求角C的大小;
(2)求△ABC的面积.
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)利用余弦的二倍角公式对已知等式整理求得cosC的值,进而求得C.
(2)利用余弦定理求得ab的值,最后利用三角形面积公式求得答案.
(2)利用余弦定理求得ab的值,最后利用三角形面积公式求得答案.
解答:
(1)解:由4cos2
-cos2C=
得
∴4•
-(2cos2C-1)=
,
整理,得4cos2C-4cosC+1=0
解得:cosC=
,
∵0°<C<180°,
∴C=60°
(2)解:由余弦定理得:c2=a2+b2-2abcosC,即7=a2+b2-ab∴7=(a+b)2-3ab
由条件a+b=5得 7=25-3ab,
∴ab=6
∴S△ABC=
absinC=
×6×
=
.
| C |
| 2 |
| 7 |
| 2 |
∴4•
| 1+cosC |
| 2 |
| 7 |
| 2 |
整理,得4cos2C-4cosC+1=0
解得:cosC=
| 1 |
| 2 |
∵0°<C<180°,
∴C=60°
(2)解:由余弦定理得:c2=a2+b2-2abcosC,即7=a2+b2-ab∴7=(a+b)2-3ab
由条件a+b=5得 7=25-3ab,
∴ab=6
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
点评:本题主要考查了余弦定理和正弦定理的运用.考查了学生分析和推理的能力.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
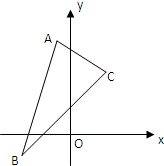 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).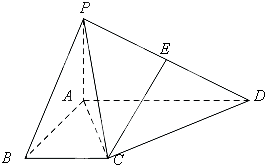 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,AD=2PA=2BC=2.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,AD=2PA=2BC=2.