题目内容
在极坐标系中,曲线C:ρsin2θ=2cosθ,过点A(5,α)(α为锐角且tanα=
)作平行于θ=
(ρ∈R)的直线l,且l与曲线C分别交于A,B两点.
(Ⅰ)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线C和直线l的普通方程;
(Ⅱ)求|AB|的长.
| 3 |
| 4 |
| π |
| 4 |
(Ⅰ)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线C和直线l的普通方程;
(Ⅱ)求|AB|的长.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由已知求出sinα,cosα的值,则由极坐标和直角坐标的互化公式求得A点的坐标,结合直线l平行于θ=
求直线l的斜率,由点斜式得直线l的方程.把曲线C:ρsin2θ=2cosθ两边同时乘以ρ,则曲线C的普通方程可求;
(Ⅱ)直接联立直线方程和曲线C的方程,利用弦长公式求得|AB|的长.
| π |
| 4 |
(Ⅱ)直接联立直线方程和曲线C的方程,利用弦长公式求得|AB|的长.
解答:
解:(Ⅰ)∵α为锐角且tanα=
,
∴sinα=
,cosα=
,
由x=5cosα=5×
=4,y=5sinα=5×
=3.
∴点A的直角坐标为(4,3),
又直线l的斜率k=tan
=1,
∴直线l的普通方程为y=x-1,
曲线C:ρsin2θ=2cosθ,得ρ2sin2θ=2ρcosθ,即y2=2x.
∴曲线C的普通方程为y2=2x;
(Ⅱ)设A(x1,y1),B(x2,y2),
联立
,得x2-4x+1=0,
由韦达定理得:x1+x2=4,x1x2=1,
由弦长公式得|AB|=
|x1-x2|
=
•
=
•
=2
.
| 3 |
| 4 |
∴sinα=
| 3 |
| 5 |
| 4 |
| 5 |
由x=5cosα=5×
| 4 |
| 5 |
| 3 |
| 5 |
∴点A的直角坐标为(4,3),
又直线l的斜率k=tan
| π |
| 4 |
∴直线l的普通方程为y=x-1,
曲线C:ρsin2θ=2cosθ,得ρ2sin2θ=2ρcosθ,即y2=2x.
∴曲线C的普通方程为y2=2x;
(Ⅱ)设A(x1,y1),B(x2,y2),
联立
|
由韦达定理得:x1+x2=4,x1x2=1,
由弦长公式得|AB|=
| 1+k2 |
=
| 2 |
| (x1+x2)2-4x1x2 |
=
| 2 |
| 42-4 |
=2
| 6 |
点评:本题是直线与圆锥曲线的综合题,考查了极坐标与直角坐标的互化,训练了利用弦长公式求线段的长度,属中档题.

练习册系列答案
相关题目
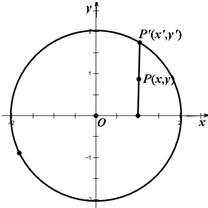 如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半 (横坐标不变),得到点P,并设点P的轨迹为曲线C.
如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半 (横坐标不变),得到点P,并设点P的轨迹为曲线C. 已知椭圆
已知椭圆 若F1、F2分别是椭圆
若F1、F2分别是椭圆