题目内容
2.如图,在矩形ABCD中,AB=1,BC=2,E为BC的中点,F为线段AD上的一点,且$AF=\frac{3}{2}$.现将四边形ABEF沿直线EF翻折,使翻折后的二面角A'-EF-C的余弦值为$\frac{2}{3}$.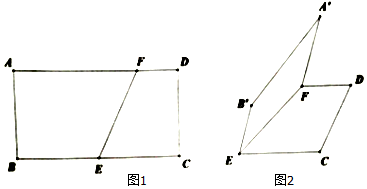
(1)求证:A'C⊥EF;
(2)求直线A'D与平面ECDF所成角的大小.
分析 (1)连接AC交EF于M点,由平面几何知识可得$AC=\sqrt{5},EF=\frac{{\sqrt{5}}}{2}$,以及$\frac{AM}{MC}=\frac{FM}{ME}=\frac{3}{2}$,经过计算可得:AM2+MF2=AF2,则AC⊥EF,再利用线面垂直的判定与性质即可证明.
(2)由(1)知,二面角A'-EF-C的平面角就是∠A'MC,即$cos∠A'MC=\frac{2}{3}$,根据余弦定理,可求得A'C=1,利用A'C2+MC2=A'M2,可得A'C⊥MC,可知A'C⊥平面ECDF,即可得出∠A'DC就是直线A'D与平面ECDF所成的角.
解答 (1)证明:连接AC交EF于M点,
由平面几何知识可得$AC=\sqrt{5},EF=\frac{{\sqrt{5}}}{2}$,
以及$\frac{AM}{MC}=\frac{FM}{ME}=\frac{3}{2}$,则有$AM=\frac{{3\sqrt{5}}}{5},MC=\frac{{2\sqrt{5}}}{5},MF=\frac{{3\sqrt{5}}}{10}$,
故有AM2+MF2=AF2,则AC⊥EF,
于是,A'M⊥EF,CM⊥EF,
而A'M∩CM=M,故EF⊥平面A'MC,
而A'C?平面A'MC,故A'C⊥EF.
(2)解:由(1)知,二面角A'-EF-C的
平面角就是∠A'MC,
即$cos∠A'MC=\frac{2}{3}$,
根据余弦定理,可求得A'C=1,
因为A'C2+MC2=A'M2,所以A'C⊥MC,
而A'C⊥EF,可知A'C⊥平面ECDF,
因此,∠A'DC就是直线A'D与平面ECDF所成的角.
由于A'C=CD=1,
故直线A'D与平面ECDF所成的角为$\frac{π}{4}$.
点评 本题考查了线面面面垂直的判定与性质定理、空间角、勾股定理的逆定理,考查了推理能力与计算能力,属于中档题.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $({-e,-\sqrt{e}})$ | B. | $({-2\sqrt{e},-e})$ | C. | $({-\sqrt{e},0})$ | D. | $[-e,-\frac{e}{2})$ |
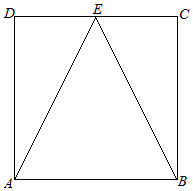 如图,点E是边长为2的正方形ABCD的CD边中点,若向正方形ABCD内随机投掷一点,则所投点落在△ABE内的概率为( )
如图,点E是边长为2的正方形ABCD的CD边中点,若向正方形ABCD内随机投掷一点,则所投点落在△ABE内的概率为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
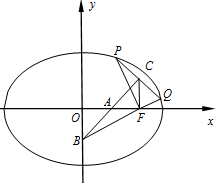 已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F的坐标为(1,0),P,Q为椭圆上位于y轴右侧的两个动点,使PF⊥QF,C为PQ中点,线段PQ的垂直平分线交x轴,y轴于点A,B(线段PQ不垂直x轴),当Q运动到椭圆的右顶点时,$|PF|=\frac{{\sqrt{2}}}{2}$.
已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F的坐标为(1,0),P,Q为椭圆上位于y轴右侧的两个动点,使PF⊥QF,C为PQ中点,线段PQ的垂直平分线交x轴,y轴于点A,B(线段PQ不垂直x轴),当Q运动到椭圆的右顶点时,$|PF|=\frac{{\sqrt{2}}}{2}$.