题目内容
17．已知复数$z=\frac{1+ai}{i}（{a∈R}）$的实部为1，则a=1，|z|=$\sqrt{2}$．分析 利用复数代数形式的乘除运算化简，由实部为1求得a值，再由复数模的求法求得|z|．
解答 解：∵z=$\frac{1+ai}{i}=\frac{（1+ai）（-i）}{-{i}^{2}}=a-i$的实部为1，
∴a=1，
则z=1-i，|z|=$\sqrt{2}$．
故答案为：1，$\sqrt{2}$．
点评 本题考查复数代数形式的乘除运算，考查复数模的求法，是基础题．
练习册系列答案
相关题目
7．将函数f（x）=sinπx的图象向左平移$\frac{1}{2}$个单位后得到函数g（x）的图象，若f（x）和g（x）在区间[-1，2]上的图象交于A，B，C三点，则△ABC的面积是（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{3\sqrt{2}}{4}$ | C． | $\sqrt{2}$ | D． | $\frac{5\sqrt{2}}{4}$ |
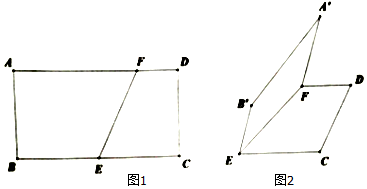
8．已知矩形ABCD，AD=$\sqrt{2}$AB，沿直线BD将△ABD折成△A′BD，使点A′在平面BCD上的射影在△BCD内（不含边界）．设二面角A′-BD-C的大小为θ，直线A′D，A′C与平面BCD所成的角分别为α，β，则（ ）
| A． | α＜θ＜β | B． | β＜θ＜α | C． | β＜α＜θ | D． | α＜β＜θ |
12．若集合A=$\left\{{x|-1＜x＜1，x∈R}\right\}，B=\left\{{x|y=\sqrt{x-2}，x∈R}\right\}$，则A∪B=（ ）
| A． | [0，1） | B． | （-1，+∞） | C． | （-1，1）∪[2，+∞） | D． | ∅ |
9．
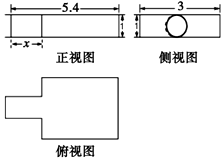我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升，其三视图如图所示（单位：寸），若π取3，且图中的x为1.6（寸）．则其体积为（ ）
我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升，其三视图如图所示（单位：寸），若π取3，且图中的x为1.6（寸）．则其体积为（ ）| A． | 0.4π+11.4立方寸 | B． | 13.8立方寸 | C． | 12.6立方寸 | D． | 16.2立方寸 |
6．在等差数列{an}中，若a2=2，a1+a5=16，则公差d等于（ ）
| A． | 4 | B． | $\frac{14}{3}$ | C． | 6 | D． | 14 |