题目内容
14.已知函数$f(x)=\frac{e^x}{x}+a({x-lnx})$,在$x∈({\frac{1}{2},2})$上有三个不同的极值点(e为自然对数的底数),则实数a的取值范围是( )| A. | $({-e,-\sqrt{e}})$ | B. | $({-2\sqrt{e},-e})$ | C. | $({-\sqrt{e},0})$ | D. | $[-e,-\frac{e}{2})$ |
分析 问题转化为ex+ax=0在x∈($\frac{1}{2}$,2)有两个不同的根,且x≠=e,令g(x)=a=-$\frac{{e}^{x}}{x}$,根据函数的单调性求出a的范围即可.
解答 解:函数的定义域为x∈(0,+∞),
f′(x)=$\frac{{(e}^{x}+ax)(x-1)}{{x}^{2}}$,
由条件可知f′(x)=0在x∈($\frac{1}{2}$,2)上有三个不同的根,
即ex+ax=0在x∈($\frac{1}{2}$,2)有两个不同的根,
令g(x)=a=-$\frac{{e}^{x}}{x}$,g′(x)=-$\frac{{e}^{x}(x-1)}{{x}^{2}}$,
x∈($\frac{1}{2}$,1)时单调递增,x∈(1,2)时单调递减,
∴g(x)max=g(1)=-e,g($\frac{1}{2}$)=-2$\sqrt{e}$,g(2)=-$\frac{1}{2}$e2,
∵-2$\sqrt{e}$-(-$\frac{1}{2}$e2)>0,
∴-2$\sqrt{e}$<a<-e,
故选:B.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.若复数$\frac{m+i}{1-i}$为纯虚数(i为虚数单位),则实数m等于( )
| A. | -1 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
9.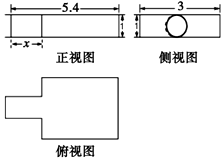 我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升,其三视图如图所示(单位:寸),若π取3,且图中的x为1.6(寸).则其体积为( )
我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升,其三视图如图所示(单位:寸),若π取3,且图中的x为1.6(寸).则其体积为( )
 我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升,其三视图如图所示(单位:寸),若π取3,且图中的x为1.6(寸).则其体积为( )
我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升,其三视图如图所示(单位:寸),若π取3,且图中的x为1.6(寸).则其体积为( )| A. | 0.4π+11.4立方寸 | B. | 13.8立方寸 | C. | 12.6立方寸 | D. | 16.2立方寸 |
6.在等差数列{an}中,若a2=2,a1+a5=16,则公差d等于( )
| A. | 4 | B. | $\frac{14}{3}$ | C. | 6 | D. | 14 |