题目内容
7.复数$z=cos\frac{2π}{3}+isin\frac{π}{3}$,则$\overline z$(其中$\overline z$为复数z的共轭复数)在复平面内对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用共轭复数的定义、几何意义即可得出.
解答 解:$z=cos\frac{2π}{3}+isin\frac{π}{3}$=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,则$\overline z$=-$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i,
在复平面内对应的点(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$)在第三象限.
故选:C.
点评 本题考查了共轭复数的定义、几何意义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知复数z满足$\frac{1+z}{i}=1-z$(i是虚数单位),则z的虚部为( )
| A. | i | B. | -1 | C. | 1 | D. | -i |
18.已知x∈R,则“|x-3|-|x-1|<2”是“x≠1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.某空间几何体的三视图如图所示,其中俯视图是半径为1的圆,则该几何体的体积是( )
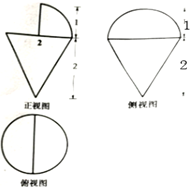

| A. | π | B. | $\frac{4π}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |
12.已知$cos({α-\frac{π}{6}})+sinα=\frac{{4\sqrt{3}}}{5}$,且$α∈({\frac{π}{2},π})$,则$sin({α+\frac{π}{3}})$的值是( )
| A. | $\frac{{4\sqrt{3}-3}}{10}$ | B. | $\frac{{4\sqrt{3}+3}}{10}$ | C. | $\frac{{3\sqrt{3}-4}}{10}$ | D. | $\frac{{3\sqrt{3}+4}}{10}$ |
16.若变量x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y-3≤0}\\{y≥1}\end{array}\right.$,则目标函数z=-2x+y的最大值为( )
| A. | 1 | B. | -1 | C. | -$\frac{3}{2}$ | D. | -3 |
12.设函数f(x)=logax(a>0,a≠1)的图象过点($\frac{1}{8}$,3),则a的值为( )
| A. | 2 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |