题目内容
10.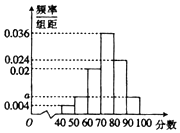 某高校在举行艺术类高考招生考试时,对100个考生进行了一项专业水平考试,考试成绩满分为100分,成绩出来后,老师对每个成绩段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]的人数进行了统计,丙得到如图所示的频率分布直方图.
某高校在举行艺术类高考招生考试时,对100个考生进行了一项专业水平考试,考试成绩满分为100分,成绩出来后,老师对每个成绩段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]的人数进行了统计,丙得到如图所示的频率分布直方图.(1)求a的值,并从频率分布直方图中求出这些成绩的中位数;
(2)为了能从分了解考生情况,对考试成绩落在[70,90)内的考生采用分层抽样的方法抽取5名考生.
(i)求在[70,80)与[80,90)内各抽取多少名考生;
(ii)如果从这5名中选出两人进行一段表演,求恰有一名考生来自[80,90)组的概率.
分析 (1)由频率分布直方图的性质求出a=0.008,由频率分布直方图得[40,70)的频率为0.32,[70,80)的频率为0.36,由此能求出这些成绩的中位数.
(2)(i)由频率分布直方图得[70,80)的频率为0.36,[80,90)的频率为0.24,对考试成绩落在[70,90)内的考生采用分层抽样的方法抽取5名考生,能求出在[70,80)与[80,90)内各抽取多少名考生.
(ii)从这5名中选出两人进行一段表演,基本事件总数n=${C}_{5}^{2}$=10,恰有一名考生来自[80,90)组包含的基本事件个数m=${C}_{3}^{1}{C}_{2}^{1}$=6,由此能求出恰有一名考生来自[80,90)组的概率.
解答 解:(1)由频率分布直方图的性质得:
(0.004+2a+0.02+0.024+0.036)×10=1,
解得a=0.008,
由频率分布直方图得[40,70)的频率为(0.004+0.008+0.02)×10=0.32,
[70,80)的频率为0.036×10=0.36,
∴这些成绩的中位数为:70+$\frac{0.5-0.32}{0.36}×10$=75.
(2)(i)由频率分布直方图得[70,80)的频率为:0.036×10=0.36,
[80,90)的频率为:0.024×10=0.24,
对考试成绩落在[70,90)内的考生采用分层抽样的方法抽取5名考生,
则在[70,80)内应抽取:5×$\frac{0.36}{0.36+0.24}$=3人,
在[80,90)内应抽取:5×$\frac{0.24}{0.36+0.24}$=2人.
(ii)从这5名中选出两人进行一段表演,
基本事件总数n=${C}_{5}^{2}$=10,
恰有一名考生来自[80,90)组包含的基本事件个数m=${C}_{3}^{1}{C}_{2}^{1}$=6,
恰有一名考生来自[80,90)组的概率p=$\frac{m}{n}=\frac{6}{10}=\frac{3}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,考查频率分直方图的性质、分层抽样、等可能事件概率计算公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

(1)求实数a的值;
(2)若k∈Z,且f(x)-k(x-1)>0对任意x>1恒成立,求k的最大值.
| A. | 5 | B. | 11 | C. | 13 | D. | 15 |
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
| 使用年数x(单位:年) | 1 | 2 | 3 | 4 | 5 |
| 维修总费用y(单位:万元) | 0.5 | 1.2 | 2.2 | 3.3 | 4.5 |
| A. | 8年 | B. | 9年 | C. | 10年 | D. | 11年 |
| A. | 1 | B. | -1 | C. | $\sqrt{2}$ | D. | -$\sqrt{2}$ |
| A. | 最大值为1 | B. | 图象关于直线x=-$\frac{π}{2}$对称 | ||
| C. | 既是奇函数又是周期函数 | D. | 图象关于点($\frac{3π}{4}$,0)中心对称 |