题目内容
8.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,直线y=kx(k>0)与椭圆C交于A,B两点,若$AF⊥BF,∠FAB∈(0,\frac{π}{12}]$,则C的离心率取值范围为( )| A. | $[\frac{{\sqrt{2}}}{2},1)$ | B. | $[\frac{{\sqrt{6}}}{3},1)$ | C. | $[\frac{{\sqrt{3}}}{3},1)$ | D. | $[\frac{2}{3},1)$ |
分析 由题意可知:四边形AFBF2是矩形.由丨BF丨=2ccosθ,丨BF2丨=丨AF丨=2csinθ,根据椭圆的定义丨BF丨+丨BF2丨=2a,即可表示出e=$\frac{1}{cosθ+sinθ}$,利用辅助角公式,及正弦函数的性质,即可求得sinθ+cosθ的取值范围,即可求得椭圆的离心率的取值范围.
解答 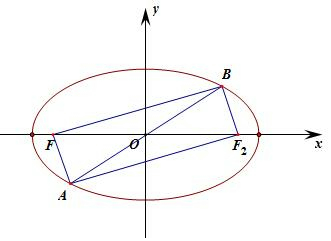 解:设F2是椭圆的右焦点,由AF⊥BF,
解:设F2是椭圆的右焦点,由AF⊥BF,
∵O点为AB的中点,丨OF丨=丨OF2丨,则四边形AFBF2是平行四边形,
∴四边形AFBF2是矩形.
如图所示设∠ABF=θ,则丨BF丨=2ccosθ,丨BF2丨=丨AF丨=2csinθ,
丨BF丨+丨BF2丨=2a,
∴2ccosθ+2csinθ=2a,
∴e=$\frac{1}{cosθ+sinθ}$,
sinθ+cosθ=$\sqrt{2}$sin(θ+$\frac{π}{4}$),
∵θ∈(0,$\frac{π}{12}$],
∴θ+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{π}{3}$],则sin(θ+$\frac{π}{4}$)∈($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$),
∴$\sqrt{2}$sin(θ+$\frac{π}{4}$)∈(1,$\frac{\sqrt{6}}{2}$),
∴e∈[$\frac{\sqrt{6}}{3}$,1).
故选B.
点评 本题考查椭圆的性质,考查椭圆的定义,辅助角公式的应用,正弦函数的性质,考查计算能力,考查数形结合思想,属于中档题.

练习册系列答案
相关题目
18.定义在(0,+∞)上的函数f(x)满足x2f′(x)+1>0,f(2)=$\frac{9}{2}$,则不等式f(lgx)<$\frac{1}{lgx}$+4的解集为( )
| A. | (10,100) | B. | (0,100) | C. | (100,+∞) | D. | (1,100) |
19.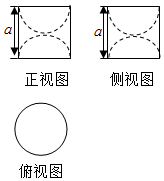 某几何体的三视图如图所示,若该几何体的体积为$\frac{2π}{3}$,则a的值为( )
某几何体的三视图如图所示,若该几何体的体积为$\frac{2π}{3}$,则a的值为( )
 某几何体的三视图如图所示,若该几何体的体积为$\frac{2π}{3}$,则a的值为( )
某几何体的三视图如图所示,若该几何体的体积为$\frac{2π}{3}$,则a的值为( )| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\root{3}{2}$ |
20.已知函数f(x)=ax+xlnx图象在点(e,f(e))(e为自然对数的底数)处的切线斜率为3.
(1)求实数a的值;
(2)若k∈Z,且f(x)-k(x-1)>0对任意x>1恒成立,求k的最大值.
(1)求实数a的值;
(2)若k∈Z,且f(x)-k(x-1)>0对任意x>1恒成立,求k的最大值.
18.已知随机变量ξ服从正态分布N(2,σ2),且P(ξ≤4-a)=P(ξ≥2+3a),则a=( )
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |