题目内容
已知f（x）=ax+bsin3x+3且f（-3）=7，则f（3）= ．
考点：正弦函数的奇偶性
专题：整体思想,函数的性质及应用
分析：根据题意，由f（-3）求出3a+bsin33的值，通过代换求出f（3）的值．
解答：
解：∵f（x）=ax+bsin3x+3，
∴f（-3）=-3a-bsin33+3=7；
∴3a+bsin33=-4，
∴f（3）=3a+bsin33+3
=-4+3
=-1．
故答案为：-1．
∴f（-3）=-3a-bsin33+3=7；
∴3a+bsin33=-4，
∴f（3）=3a+bsin33+3
=-4+3
=-1．
故答案为：-1．
点评：本题考查了求函数值的问题，解题时应用代换的方法，即可求出正确的结果，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
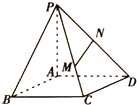如图所示，已知矩形ABCD，P为平面ABCD外一点，且PA⊥面ABCD，M、N分别为PC，PD上的点，且PM：MC=2：1，N为PD的中点，则满足