题目内容
对任意实数x,<x>表示不小于x的最小整数,如<1.1>=2,<-1.1>=-1,则“|x-y|<1”是“<x>=<y>”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充分 |
| D、既不充分又不必要 |
考点:必要条件、充分条件与充要条件的判断
专题:计算题,简易逻辑
分析:通过举反例说明|x-y|<1推不出<x>=<y>,证明由<x>=<y>可推出|x-y|<1.
解答:
解:若x=1.6,y=2.1,
则|x-y|<1,但<x>=2≠<y>=3,
又∵若<x>=<y>,
则x,y同时在同一组相邻的整数之间,
则|x-y|<1,
故“|x-y|<1”是“<x>=<y>”的必要不充分条件,
故选B.
则|x-y|<1,但<x>=2≠<y>=3,
又∵若<x>=<y>,
则x,y同时在同一组相邻的整数之间,
则|x-y|<1,
故“|x-y|<1”是“<x>=<y>”的必要不充分条件,
故选B.
点评:本题考查了充分必要条件的判断,属于基础题.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
在△ABC中,若AB=4,BC=2
,且
•
=-8,则AC等于( )
| 2 |
| BA |
| BC |
A、4
| ||
| B、4 | ||
C、2
| ||
D、2
|
P是椭圆
+
=1上一点,F1,F2分别为左、右焦点,△PF1F2的内切圆的半径为1,则|
+
|的值为( )
| x2 |
| 25 |
| y2 |
| 9 |
| PF1 |
| PF2 |
| A、8 | ||||
B、4
| ||||
| C、4 | ||||
D、
|
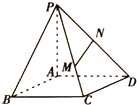 如图所示,已知矩形ABCD,P为平面ABCD外一点,且PA⊥面ABCD,M、N分别为PC,PD上的点,且PM:MC=2:1,N为PD的中点,则满足
如图所示,已知矩形ABCD,P为平面ABCD外一点,且PA⊥面ABCD,M、N分别为PC,PD上的点,且PM:MC=2:1,N为PD的中点,则满足