题目内容
11.在△ABC中,$∠A=\frac{2π}{3}$,$a=\sqrt{3}c$,则$\frac{a}{b}$=$\sqrt{3}$.分析 由正弦定理可求sinC的值,结合C的范围可求C,利用三角形内角和定理可求B,由正弦定理及比例的性质即可计算得解.
解答 解:∵$∠A=\frac{2π}{3}$,$a=\sqrt{3}c$,
∴由正弦定理$\frac{a}{sinA}=\frac{c}{sinC}$,可得:$\frac{\sqrt{3}c}{\frac{\sqrt{3}}{2}}$=$\frac{c}{sinC}$,解得:sinC=$\frac{1}{2}$,C为锐角,可得C=$\frac{π}{6}$,
∴由A+B+C=π,可得:B=$\frac{π}{6}$,
∴$\frac{a}{b}$=$\frac{sinA}{sinB}$=$\frac{sin\frac{2π}{3}}{sin\frac{π}{6}}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题主要考查了正弦定理,三角形内角和定理及比例的性质的综合应用,考查了转化思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅下表来确定断言“X和Y有关系”的可信度.如果k>5.024,那么就有把握认为“X和Y有关系”的百分比为97.5%.
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| P(K2≥k) | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
19.如图(1),五边形PABCD是由一个正方形与一个等腰三角形拼接而成,其中∠APD=120°,AB=2,现将△PAD进行翻折,使得平面PAD⊥平面ABCD,连接PB,PC,所得四棱锥P-ABCD如图(2)所示,则四棱锥P-ABCD的外接球的表面积为( )
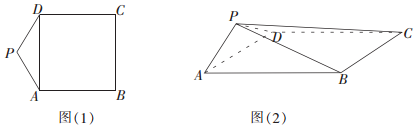

| A. | $\frac{14}{3}π$ | B. | $\frac{7}{3}π$ | C. | $\frac{28}{3}π$ | D. | 14π |
6.在2L高产优质小麦种子中混入了一粒带白粉病的种子,从中随机取出10mL,则含有白粉病种子的概率是( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{50}$ | C. | $\frac{1}{100}$ | D. | $\frac{1}{200}$ |
 已知圆锥的侧面展开图是一个半圆;
已知圆锥的侧面展开图是一个半圆;