题目内容
20.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.(1)根据以上数据建立一个2×2的列联表;
(2)是否有97.5%的把握认为性别与休闲方式有关系?
分析 (1)利用已知条件建立一个2×2的列联表;
(2)利用独立检验公式求出k,判断即可.
解答 解:(1)2×2的列联表
| 性别 休闲方式 | 看电视 | 运动 | 总计 |
| 女 | 43 | 27 | 70 |
| 男 | 21 | 33 | 54 |
| 总计 | 64 | 60 | 124 |
计算K=$\frac{124×(43×33-27×21)^{2}}{70×54×64×60}$≈6.201
因为K≥5.024,所以有理由认为假设“休闲方式与性别无关”是不合理的,
即有97.5%的把握认为“休闲方式与性别有关”
点评 本题考查联列表的画法,独立检验的应用,考查计算能力.

练习册系列答案
相关题目
11.${∫}_{-1}^{1}$x2dx=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
8.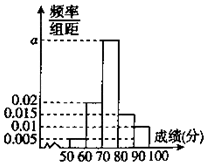 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
(1)求a和n的值;
(2)设成绩在80分以上(含80分)为优秀,已知样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,请完成下面的2×2列联表,并判断是否有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.(1)求a和n的值;
(2)设成绩在80分以上(含80分)为优秀,已知样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,请完成下面的2×2列联表,并判断是否有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
| k | 0.455 | 3.841 | 5.024 | 7.879 |
| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
10.若函数f(x)=sin(2x+φ)满足?x∈R,f(x)≤f($\frac{π}{6}$),则f(x)在[0,π]上的单调递增区间为( )
| A. | [0,$\frac{π}{6}$]与[$\frac{π}{2}$,$\frac{2π}{3}$] | B. | [$\frac{π}{3}$,$\frac{2π}{3}$] | C. | [0,$\frac{π}{6}$]与[$\frac{2π}{3}$,π] | D. | [0,$\frac{π}{6}$]与[$\frac{π}{3}$,$\frac{2π}{3}$] |
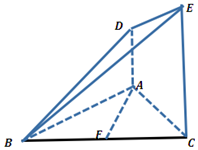 如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,
如图,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,四边形ACED的面积为$\frac{3}{2}$,F为BC的中点,