题目内容
4.已知等差数列{an}的前n项和为Sn,且a1=1,S3+S4=S5.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=(-1)n-1anan+1,求数列{bn}的前2n项和T2n.
分析 (Ⅰ)设等差数列{an}的公差为d,根据题意、等差数列的性质以及通项公式列出方程,求出公差d,由等差数列的通项公式求出an;
(Ⅱ)由(I)化简bn=(-1)n-1anan+1,利用并项求和法和等差数列的前n项和公式求出数列{bn}的前2n项和T2n.
解答 解:(Ⅰ)设等差数列{an}的公差为d,
由S3+S4=S5可得a1+a2+a3=a5,-------(2分)
即3a2=a5,则3(1+d)=1+4d,解得d=2-----(4分)
所以an=1+(n-1)×2=2n-1.------------(6分)
(Ⅱ)由(Ⅰ)可得:
${b_n}={(-1)^{n-1}}•(2n-1)(2n+1)={(-1)^{n-1}}•(4{n^2}-1)$------(7分)
所以${T_{2n}}=(4×{1^2}-1)-(4×{2^2}-1)+(4×{3^2}-1)-(4×{4^2}-1)+…+{(-1)^{2n-1}}•[{4×{{(2n)}^2}-1}]$
=4[12-22+32-42+…+(2n-1)2-(2n)2]------------(9分)
=-4(1+2+3+4+…+2n-1+2n)
=$-4×\frac{2n(2n+1)}{2}=-8{n}^{2}-4n$------(12分)
点评 本题考查等差数列的性质、通项公式以及前n项和公式,以及并项求和法求数列的和,考查化简、变形能力.

练习册系列答案
相关题目
19.执行如图所示的程序框图,输出S的值为( )
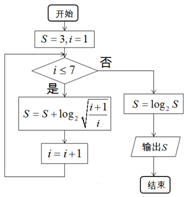

| A. | log210-1 | B. | 2log23-1 | C. | $\frac{9}{2}$ | D. | 6 |
9.在等差数列{an}中,a1=1,a3+a4+a5+a6=20,则a8=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
 ,且
,且 ,则
,则 的值是 ( )
的值是 ( ) C.
C. D.400
D.400