已知向量$\overrightarrow{a}$=.$\overrightarrow{b}$=.且$\overrightarrow{a}$∥$\overrightarrow{b}$.计算:$\frac{sinα+2cosα}{cosα-3sinα}$．题目和参考答案——青夏教育精英家教网—

题目内容

6．已知向量$\overrightarrow{a}$=（1，sinα），$\overrightarrow{b}$=（2，cosα），且$\overrightarrow{a}$∥$\overrightarrow{b}$，计算：$\frac{sinα+2cosα}{cosα-3sinα}$．

分析根据向量平行建立方程关系，代入进行化简即可．

解答解：∵$\overrightarrow{a}$∥$\overrightarrow{b}$，∴2sinα-cosα=0，即cosα=2sinα，
则$\frac{sinα+2cosα}{cosα-3sinα}$=$\frac{sinα+4sinα}{2sinα-3sinα}$=$\frac{5sinα}{-sinα}$=-5．

点评本题主要考查三角函数式的化简和求值，根据向量共线的等价条件进行等量代换是解决本题的关键．比较基础．

练习册系列答案

学段衔接提升方案赢在高考寒假作业系列答案

新校园快乐假期系列寒假生活指导系列答案

相关题目

16．某个几何体的三视图如图所示，则该几何体的体积是1．

17．已知抛物线C：y²=2px（p＞0）的焦点为F，C上一点（3，m）到焦点的距离为5．
（1）求C的方程；
（2）过F作直线l，交C于A、B两点，若线段AB中点的纵坐标为-1，求直线l的方程．

14．某个几何体的三视图如图所示，则该几何体的体积是1

1．在正方体ABCD-A₁B₁C₁D₁中，若棱长AB=3，则点B到平面ACD₁的距离为$\sqrt{3}$．

11．对于数25，规定第1次操作为2³+5³=133，第2次操作为1³+3³+3³=55，如此反复操作，则第2016次操作后得到的数是（　　）

18．执行如图所示的程序框图，若输入p的值是6，则输出S的值是$\frac{31}{32}$．

15．

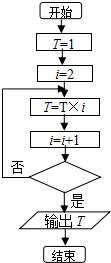若如图程序框图的输出结果为120，则判断框中应填写的判断条件为（　　）

16．

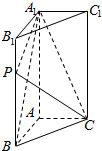如图，在直三棱柱ABC-A₁B₁C₁中，底面△ABC是直角三角形，AB=AC=1，AA₁=2，点P是棱BB₁上一点，满足$\overrightarrow{BP}$=λ$\overrightarrow{B{B}_{1}}$（0≤λ≤1）．
（1）若$λ=\frac{1}{3}$，求直线PC与平面A₁BC所成角的正弦值；
（2）若二面角P-A₁C-B的正弦值为$\frac{2}{3}$，求λ的值．

试题分类