题目内容
下列说法中,正确的是 .
①任取x∈R,均有3x>2x;
②当a>0,且a≠1时,有a3>a2;
③y=(
)-x是增函数;
④y=2|x|的最小值为1;
⑤在同一坐标系中,y=2x与y=2-x的图象关于y轴对称.
①任取x∈R,均有3x>2x;
②当a>0,且a≠1时,有a3>a2;
③y=(
| 3 |
④y=2|x|的最小值为1;
⑤在同一坐标系中,y=2x与y=2-x的图象关于y轴对称.
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①,举例说明,如3-1<2-1,可判断①;
②,举例说明,如(0.1)3<(0.1)2,可判断②;
③,利用指数函数的单调性可判断y=(
)-x是减函数;
④,由y=2|x|≥1可判断④;
⑤,利用指数函数的性质,可判断⑤.
②,举例说明,如(0.1)3<(0.1)2,可判断②;
③,利用指数函数的单调性可判断y=(
| 3 |
④,由y=2|x|≥1可判断④;
⑤,利用指数函数的性质,可判断⑤.
解答:
解:对于①,任取x∈R,均有3x>2x,错误,如3-1<2-1,故①错误;
对于②,当a>0,且a≠1时,有a3>a2;错误,如(0.1)3<(0.1)2,故②错误;
对于③,y=(
)-x=(
)x是减函数,故③错误;
对于④,y=2|x|的≤20=1,即y的最小值为1,故④正确;
对于⑤,在同一坐标系中,y=2x与y=2-x的图象关于y轴对称,显然正确.
故答案为:④⑤.
对于②,当a>0,且a≠1时,有a3>a2;错误,如(0.1)3<(0.1)2,故②错误;
对于③,y=(
| 3 |
| ||
| 3 |
对于④,y=2|x|的≤20=1,即y的最小值为1,故④正确;
对于⑤,在同一坐标系中,y=2x与y=2-x的图象关于y轴对称,显然正确.
故答案为:④⑤.
点评:本题考查指数函数、幂函数的性质,熟练掌握基本初等函数的图象与性质,是解决问题的关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知直线l经过两条直线2x-y+6=0和3x+y+4=0的交点
(1)若直线l与直线3x-4y+4=0垂直,求直线l的方程
(2)若直线m与(1)中所求直线l平行,且m与l之间的距离为2,求直线m的方程.
(1)若直线l与直线3x-4y+4=0垂直,求直线l的方程
(2)若直线m与(1)中所求直线l平行,且m与l之间的距离为2,求直线m的方程.
已知集合M={x|y=lg
},N={y|y=x2+2x+3},则(∁RM)∩N=( )
| 1-x |
| x |
| A、{x|10<x<1} |
| B、{x|x>1} |
| C、{x|x≥2} |
| D、{x|1<x<2} |
设全集U=R,且A={x||x-1|>2},B={x|x2-6x+8<0},则(∁UA)∩B=( )
| A、[-1,4) |
| B、(2,3) |
| C、(2,3] |
| D、(-1,4) |
若α是三角形的一个内角,且sinα+cosα=
,则三角形的形状为( )
| 1 |
| 5 |
| A、钝角三角形 | B、锐角三角形 |
| C、直角三角形 | D、无法确定 |
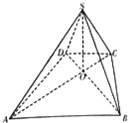 如图所示,四棱锥S-ABCD的底面ABCD为等腰梯形,AB∥CD,对角线AC与BD交于点O,OA=3,OD=1,CD=
如图所示,四棱锥S-ABCD的底面ABCD为等腰梯形,AB∥CD,对角线AC与BD交于点O,OA=3,OD=1,CD=