题目内容
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的焦距为$2\sqrt{5}$,且双曲线的一条渐近线方程为x-2y=0,则双曲线的方程为( )| A. | $\frac{x^2}{4}-{y^2}=1$ | B. | $\frac{3{x}^{2}}{20}$-$\frac{3{y}^{2}}{5}$=1 | C. | $\frac{{3{x^2}}}{20}-\frac{{3{y^2}}}{5}=1$ | D. | $\frac{{3{x^2}}}{5}-\frac{{3{y^2}}}{20}=1$ |
分析 利用双曲线的焦距以及渐近线方程,推出a,b的方程,求解即可得到双曲线方程.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的焦距为$2\sqrt{5}$,可得c=$\sqrt{5}$,即a2+b2=5,…①
双曲线的一条渐近线方程为x-2y=0,可得a=2b,…②,
解①②可得a=2,b=1.
所求的双曲线方程为:$\frac{x^2}{4}-{y^2}=1$.
故选:A.
点评 本题考查双曲线的简单性质的应用,双曲线方程的求法,考查计算能力.

练习册系列答案
相关题目
17.圆x2+y2-2x-8y+13=0与直线ax+y-1=0的相交所得弦长为2$\sqrt{3}$,则a=( )
| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
18.已知双曲线的一条渐近线过点$({2,\sqrt{3}})$,且双曲线的一个焦点在抛物线${x^2}=4\sqrt{7}y$的准线上,则双曲线的标准方程为( )
| A. | $\frac{y^2}{3}-\frac{x^2}{4}=1$ | B. | $\frac{y^2}{4}-\frac{x^2}{3}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
2.已知集合A={x|x2-x-2≤0},B=Z,则A∩B=( )
| A. | {-1,0,1,2} | B. | {-2,-1,0,1} | C. | {0,1} | D. | {-1,0} |
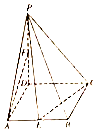 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=4,点E、F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=4,点E、F分别为AB和PD的中点.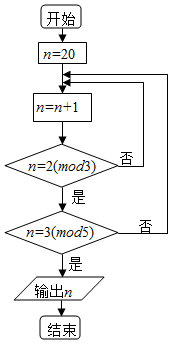 中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( )
中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( )