题目内容
15.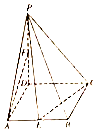 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=4,点E、F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=4,点E、F分别为AB和PD的中点.(1)求证:直线AF∥平面PEC;
(2)求平面PAD与平面PEC所成锐二面角的正切值.
分析 (1)取PC中点Q,连接EQ,FQ,推导出四边形AEQF是平行四边形,从而AF∥EQ,由此能证明直线AF∥平面PEC.
(2)以D为原点,DE为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,利用向量法平面PAD与平面PEC所成锐二面角的正切值.
解答 证明:(1)取PC中点Q,连接EQ,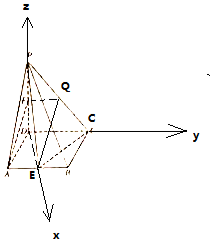 FQ,
FQ,
∵点E、F分别为AB和PD的中点,底面ABCD为菱形,
∴FQ$\underset{∥}{=}$$\frac{1}{2}AB$=AE,∴FQ$\underset{∥}{=}$AE,
∴四边形AEQF是平行四边形,
∴AF∥EQ,
∵AF?平面PEC,EQ?平面PEC,
∴由线面平行的判定定理得直线AF∥平面PEC.
解:(2)以D为原点,DE为x轴,DC为y轴,DP为z轴,建立空间直角坐标系,
P(0,0,4),E(2$\sqrt{3}$,0,0),C(0,4,0),
$\overrightarrow{PE}$=(2$\sqrt{3}$,0,-4),$\overrightarrow{EC}$=(-2$\sqrt{3}$,4,0),
设平面PEC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PE}=2\sqrt{3}x-4z=0}\\{\overrightarrow{n}•\overrightarrow{EC}=-2\sqrt{3}x+4y=0}\end{array}\right.$,取x=2,得$\overrightarrow{n}$=(2,$\sqrt{3},\sqrt{3}$),
∴面PEC的法向量$\overrightarrow n=(2,\sqrt{3},\sqrt{3})$
同理得面PAD的法向量$\overrightarrow m=(1,\sqrt{3},0)$,
设所求二面角为α,则$cosα=|{cos<\overrightarrow m,\overrightarrow{n>}}|=\frac{{\sqrt{10}}}{4}$,
∴$sinα=\frac{{\sqrt{6}}}{4}∴tanα=\frac{{\sqrt{15}}}{5}$.
故平面PAD与平面PEC所成锐二面角的正切值为$\frac{\sqrt{15}}{5}$.
点评 本题考查线面平行的证明,考查二面角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | $\frac{x^2}{4}-{y^2}=1$ | B. | $\frac{3{x}^{2}}{20}$-$\frac{3{y}^{2}}{5}$=1 | C. | $\frac{{3{x^2}}}{20}-\frac{{3{y^2}}}{5}=1$ | D. | $\frac{{3{x^2}}}{5}-\frac{{3{y^2}}}{20}=1$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |