题目内容
5.设数列{an}的前n项和为Sn,已知a1=1,Sn-Sn-1=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$(n≥2),求an.分析 构造并可判断数列{$\sqrt{{S}_{n}}$}是以1为首项,1为公差的等差数列,从而求Sn,再求an.
解答 解:∵Sn-Sn-1=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$,
∴($\sqrt{{S}_{n}}$-$\sqrt{{S}_{n-1}}$)($\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$)=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$,
∴$\sqrt{{S}_{n}}$-$\sqrt{{S}_{n-1}}$=1,
而$\sqrt{{S}_{1}}$=1,
故数列{$\sqrt{{S}_{n}}$}是以1为首项,1为公差的等差数列,
故$\sqrt{{S}_{n}}$=n,
故Sn=n2,
当n≥2时,an=Sn-Sn-1=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$=n+n-1=2n-1,
当n=1时也满足an=2n-1;
故an=2n-1.
点评 本题考查了数列的递推式的应用及构造法的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在△ABC中,若sin(B+C)=2sinBcosC,那么这个三形一定是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰三角形 |
13.若集合M={x|$\frac{1}{x}$<2},集合N={x|-1<x<2},则M∩N等于( )
| A. | {x|$\frac{1}{2}$<x<2} | B. | {x|-1<x<0或$\frac{1}{2}$<x<2} | C. | {x|-1<x<$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$或1<x<2} |
 设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.
设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.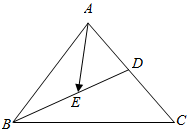 如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.
如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.