Question

已知向量

a

=（1，0），

b

=（x，

3-(x-2)2

），设

a

，

b

的夹角为θ，则cosθ的值域为（　　）

• A、[

  1

  2

  ，1]
• B、[0，

  1

  2

  ]
• C、[0，

  3

  2

  ]
• D、[

  3

  2

  ，1]

Answer 1

考点：平面向量数量积的运算

专题：计算题,平面向量及应用,直线与圆

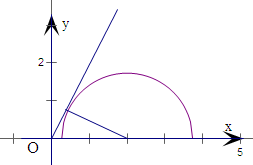
分析：令y=

3-(x-2)2

，即有（x-2）²+y²=3（y≥0），表示圆心为（2，0），半径为

3

的上半圆．则

b

的终点在上半圆上，画出图象，通过观察即可得到夹角范围．

解答： 解：由于

b

=（x，

3-(x-2)2

），
令y=

3-(x-2)2

，即有（x-2）²+y²=3（y≥0），
表示圆心为（2，0），半径为

3

的上半圆．
则

b

的终点在上半圆上，
当向量

b

与半圆相切时，切线的倾斜角为

π

3

，
则有

a

，

b

的夹角为θ∈[0，

π

3

]，
cosθ∈[

1

2

，1]．
故选A．

点评：本题考查向量的夹角的求法，考查直线和圆的位置关系，考查数形结合的能力，属于中档题．