Question

设函数f（x）=xcosx在（0，+∞）内的全部极值点按从小到大的顺序排列为x₁，x₂，…则对任意正整数n必有（　　）

• A、-

  π

  2

  ＜xn+1-xn＜0
• B、

  π

  2

  ＜xn+1-xn＜π
• C、0＜xn+1-xn＜

  π

  2

• D、π＜xn+1＜xn＜

  3π

  2

Answer 1

考点：利用导数研究函数的极值

专题：计算题,作图题,导数的综合应用,三角函数的图像与性质

分析：先求导并令导数f'（x）=cosx-xsinx=0得cosx-xsinx=0，从而得

1

x

=tanx，从而知方程

1

x

=tanx的实根就是f（x）的极值点，从而借助图象求解．

解答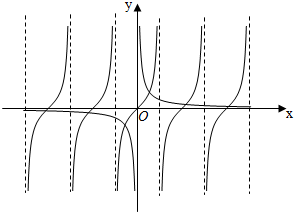： 解：由f'（x）=cosx-xsinx=0得cosx-xsinx=0，
显然cosx≠0，
所以

1

x

=tanx，
易知方程

1

x

=tanx的实根就是f（x）的极值点．
在除(-

π

2

，

π

2

)外的正切函数的每一个周期内，
y=

1

x

与y=tanx的图象有且只有一个交点，
在（0，+∞）上设相邻两个交点的坐标为（x_n，y_n），（x_n+1，y_n+1）
，因为y=

1

x

在（0，+∞）上单调递减，
所以当x_n＜x_n+1时，y_n＞y_n+1，
即tanx_n+1＜tanx_n=tan（x_n+π），
而y=tanx在每一个周期上都是单调递增，
所以x_n+1＜x_n+π，
故x_n+1-x_n＜π． 
又y_n＞0，y_n+1＞0，
故xn∈(kπ，kπ+

π

2

)，xn+1∈((k+1)π，(k+1)π+

π

2

)，
因此

π

2

＜xn+1-xn＜

3π

2

，
综上得

π

2

＜xn+1-xn＜π，
故选B．

点评：本题考查了导数的综合应用及三角函数的性质与应用，同时考查了数形结合的思想，属于中档题．