题目内容

若x，y满足约束条件
x+y≥1
x-y≥-1
2x-y≤2

（Ⅰ）求目标函数z=x-2y的值域；
（Ⅱ）若目标函数z=λx+2y仅在点（1，0）处取得最小值，求λ的取值范围．
考点：简单线性规划
专题：数形结合,不等式的解法及应用
分析：（Ⅰ）由约束条件作出可行域，通过平移直线x-2y=0可得目标函数z=x-2y的值域；
（Ⅱ）由可行域直接得到-1＜-
λ
2
＜2，则λ的取值范围可求．
解答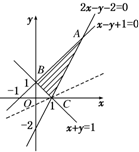： 解：（Ⅰ）由约束条件
x+y≥1
x-y≥-1
2x-y≤2
作出可行域如图，
可求得A（3，4），B（0，1），C（1，0）．
平移初始直线x-2y=0，过A（3，4）取最小值-5，过C（1，0）取最大值1．
∴z的最大值为1，最小值为-2．故所求值域为[-5，1]；
（Ⅱ）直线λx+2y-z=0仅在点（1，0）处取得最小值，
由图象可知-1＜-
λ
2
＜2，
解得-4＜λ＜2．
故所求λ的取值范围为（-4，2）．
点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
已知n（n∈N*）满足3
C
n-5
n-1
=5
P
2
n-2
，整数a是413+
C
1
13
412+
C
2
13
411+…+
C
12
13
4除以6的余数．
（1）求n和a的值；
（2）求(x2+
a
x
)n二项展开式中二项式系数最大的项；
（3）利用二项式定理，求函数F(x)=(x2+
a
x
)5+(
1
x2
+ax)5在区间[
1
2
，2]上的最小值．
平面向量
a
=（-4，4），
b
=（2，x），
c
=（2，y），已知
a
∥
b
，
a
⊥
c
，
（1）求（2
a
+
b
）•
c
的值；
（2）求 
b
+
a
与
c
夹角的余弦值．
计算：
lim
x→-∞
（x4+x5）=
 
．
在△ABC中，角A，B，C所对的边分别为a，b，c，
m
=（sin（x-A），sinA），
n
=（2cosx，1）（x∈R），函数f（x）=
m
•
n
在x=
5π
12
处取得最大值．
（1）当x∈（0，
π
2
）时，求函数f（x）的值域；
（2）若a=7且sinB+sinC=
13
3
14
，求△ABC的面积．
满足tan(4x-
π
4
)=1的锐角x的集合为
 
．
在△ABC中，“A=
π
3
”是“cosA=
1
2
”的（　　）
A、充分而不必要条件
B、必要而不充分条件
C、充分必要条件
D、既不充分也不必要条件
若直线l：ax+y+1=0平分圆x2+y2-2x+6y+5=0的面积，则直线l的倾斜角为
 
．（用反三角函数值表示）
已知集合P={1，2，3}，Q={2，3，4，5}}，则集合P∩Q为（　　）
A、{1，2，3}
B、{2，3，4}
C、{3，4，5}
D、{2，3}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网