题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,
=(sin(x-A),sinA),
=(2cosx,1)(x∈R),函数f(x)=
•
在x=
处取得最大值.
(1)当x∈(0,
)时,求函数f(x)的值域;
(2)若a=7且sinB+sinC=
,求△ABC的面积.
| m |
| n |
| m |
| n |
| 5π |
| 12 |
(1)当x∈(0,
| π |
| 2 |
(2)若a=7且sinB+sinC=
13
| ||
| 14 |
考点:两角和与差的正弦函数,三角函数的最值
专题:计算题,解三角形
分析:(1)化简可得f(x)=sin(2x-A).由已知可解得A的值,由x∈(0,
)从而确定函数f(x)的值域;
(2)由已知及由正弦定理得2R=
=
,可解得b+c=13,由余弦定理得,a2=b2+c2-2bccosA,解得bc=40,从而可求△ABC的面积.
| π |
| 2 |
(2)由已知及由正弦定理得2R=
| a |
| sinA |
14
| ||
| 3 |
解答:
解:(1)f(x)=
•
=2cosxsin(x-A)+sinA=2cosxsinxcosA-2cos2xsinA+sinA=sin2xcosA-sinAcos2x=sin(2x-A).
∵函数f(x)=
•
在x=
处取得最大值.
∴2×
-A+2kπ=
,可解得A=
+2kπ,不妨取A=
.
∴f(x)=sin(2x-
).
∵x∈(0,
)
∴-
<2x-
<
∴-
<sin(2x-
)≤1.
∴函数f(x)的值域为(-
,1].
(2)∵a=7,sinA=sin
=
设△ABC的外接圆的半径为R,
则由正弦定理得,2R=
=
,
由sinB+sinC=
,得
+
=
,即b+c=13,
由余弦定理得,a2=b2+c2-2bccosA,
即49=(b+c)2-3bc,
解得bc=40,
所以△ABC的面积S△ABC=
bcsinA=
×40×
=10
.
| m |
| n |
∵函数f(x)=
| m |
| n |
| 5π |
| 12 |
∴2×
| 5π |
| 12 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
∴f(x)=sin(2x-
| π |
| 3 |
∵x∈(0,
| π |
| 2 |
∴-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴-
| ||
| 2 |
| π |
| 3 |
∴函数f(x)的值域为(-
| ||
| 2 |
(2)∵a=7,sinA=sin
| π |
| 3 |
| ||
| 2 |
设△ABC的外接圆的半径为R,
则由正弦定理得,2R=
| a |
| sinA |
14
| ||
| 3 |
由sinB+sinC=
13
| ||
| 14 |
| b |
| 2R |
| c |
| 2R |
13
| ||
| 14 |
由余弦定理得,a2=b2+c2-2bccosA,
即49=(b+c)2-3bc,
解得bc=40,
所以△ABC的面积S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评:本题主要考察了两角和与差的正弦函数,三角函数的最值,属于基本知识的考查,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知锐角△ABC中,角A、B、C的对边长分别为a、b、c,向量
=(cosC+sinC,1),
=(cosC-sinC,
),且
⊥
.
(1)求角C的大小;
(2)若边c=2,求△ABC面积的最大值.
| m |
| n |
| 1 |
| 2 |
| m |
| n |
(1)求角C的大小;
(2)若边c=2,求△ABC面积的最大值.
若函数f(x)=log2(x2-2ax+3)在区间(-∞,1]内单调递减,则a的取值范围是( )
| A、[1,+∞) |
| B、(1,+∞) |
| C、[1,2) |
| D、[1,2] |
若A,B,C分别为△ABC的三个内角,且sinA:sinB:sinC=3:5:7,则△ABC的最大内角是( )
| A、135° | B、90° |
| C、120° | D、150° |
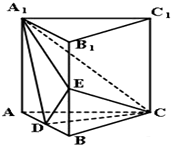 如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°.E为的中点,D点在AB上且DE=
如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°.E为的中点,D点在AB上且DE=