题目内容
15.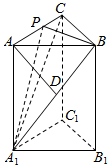 如图,在直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.
如图,在直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.(Ⅰ)求证:BC⊥A1B;
(Ⅱ)若P是线段AC上一点,$AD=\sqrt{3}$,AB=BC=2,三棱锥A1-PBC的体积为$\frac{{\sqrt{3}}}{3}$,求$\frac{AP}{PC}$的值.
分析 (I)由AD⊥平面A1BC得BC⊥AD,由AA1⊥平面ABC得BC⊥AA1,故BC⊥平面A1AB,所以BC⊥A1B;
(II)设PC=x,用x表示出棱锥A1-BPC的体积,列出方程解出x,得到AP和PC的值.
解答  (Ⅰ)证明∵AD⊥平面A1BC,BC?平面A1BC,
(Ⅰ)证明∵AD⊥平面A1BC,BC?平面A1BC,
∴AD⊥BC.
∵AA1⊥平面ABC,BC?平面ABC,
∴AA1⊥BC.
又∵AA1∩AD=A,AA1?平面AA1B,AD?平面AA1B,
∴BC⊥平面AA1B,∵A1B?平面AA1B,
∴BC⊥A1B.
(Ⅱ)解:设PC=x,过点B作BE⊥AC于点E.
由(Ⅰ)知BC⊥平面AA1B1B,∴BC⊥AB,
∵AB=BC=2,∴$AC=2\sqrt{2}$,$BE=\sqrt{2}$.
∴${S_{△PBC}}=\frac{1}{2}BE•CP=\frac{{\sqrt{2}}}{2}x$,
∵AD⊥平面A1BC,其垂足D落在直线A1B上,
∴AD⊥A1B.∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=1,又∵AA1⊥AB,
∴Rt△ABD∽Rt△A1BA,∴$\frac{BD}{AB}=\frac{AD}{A{A}_{1}}$,
∴$A{A_1}=2\sqrt{3}$.
∴${V_{{A_1}-PBC}}=\frac{1}{3}{S_{△PBC}}•A{A_1}=\frac{{\sqrt{6}}}{3}x$=$\frac{\sqrt{3}}{3}$.
解得:$x=\frac{{\sqrt{2}}}{2}$,
∴$AP=\frac{{3\sqrt{2}}}{2}$.∴$\frac{AP}{PC}=3$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
8.已知函数f(x)=sinx+λcosx(λ∈R)的图象关于直线x=-$\frac{π}{4}$对称,把函数f(x)的图象上,每个点的横坐标扩大到原来的2倍,纵坐标不变,再将所得函数图象向右平移$\frac{π}{3}$个单位长度,得到函数g(x)的图象,则函数g(x)的一个对称中心是( )
| A. | ($\frac{π}{6}$,0) | B. | ($\frac{π}{4}$,0) | C. | ($\frac{2π}{3}$,0) | D. | ($\frac{5π}{6}$,0) |
7.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与直线y=x交于不同的两点,则双曲线C的离心率的取值范围是( )
| A. | (1,$\sqrt{2}$)∪($\sqrt{2}$,+∞) | B. | ($\sqrt{2}$,+∞) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
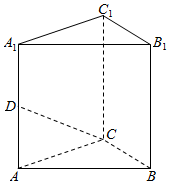 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,BC=1,$∠BAC=\frac{π}{6}$,D为棱AA1中点,证明异面直线B1C1与CD所成角为$\frac{π}{2}$,并求三棱柱ABC-A1B1C1的体积.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,BC=1,$∠BAC=\frac{π}{6}$,D为棱AA1中点,证明异面直线B1C1与CD所成角为$\frac{π}{2}$,并求三棱柱ABC-A1B1C1的体积.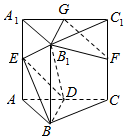 三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,各棱长均为2,D,E,F,G分别是棱AC,AA1,CC1,A1C1的中点.
三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,各棱长均为2,D,E,F,G分别是棱AC,AA1,CC1,A1C1的中点.