题目内容
4.已知集合A={x|2a+1≤x<3a+5},B={x|3≤x≤32},若A⊆(A∩B),求a的取值范围.分析 由A⊆(A∩B),可得A⊆B,再分类讨论,即可求a的取值范围.
解答 解:∵A⊆(A∩B),∴A⊆B.
①A=∅,2a+1≥3a+5,∴a≤-4…(4分)
②A≠∅,3≤2a+1,3a+5≤32,∴1≤a≤9,…(4分)
综上所述,a≤-4或1≤a≤9.
点评 本题考查集合的关系与运算,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
12.已知点(2,1)在双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线上,则C的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | $\frac{\sqrt{5}}{2}$ |
19.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为2x-y=0,则它的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
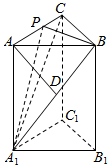 如图,在直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.
如图,在直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.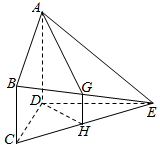 已知:如图所示,平面ABCD⊥平面CDE,BC∥AD,∠BCD=90°,CD⊥DE,AD=DC=DE=2BC=2,G,H分别是BE,CE的中点.
已知:如图所示,平面ABCD⊥平面CDE,BC∥AD,∠BCD=90°,CD⊥DE,AD=DC=DE=2BC=2,G,H分别是BE,CE的中点. 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知:∠ABC=45°,AB=2,$BC=2\sqrt{2}$,SB=SC,直线SA与平面ABCD所成角为45°,O为BC的中点.
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知:∠ABC=45°,AB=2,$BC=2\sqrt{2}$,SB=SC,直线SA与平面ABCD所成角为45°,O为BC的中点.