题目内容
7.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与直线y=x交于不同的两点,则双曲线C的离心率的取值范围是( )| A. | (1,$\sqrt{2}$)∪($\sqrt{2}$,+∞) | B. | ($\sqrt{2}$,+∞) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
分析 将直线y=x代入双曲线的方程,由题意可得b2-a2>0,再由a,b,c的关系和离心率公式即可得到所求范围.
解答 解:将直线y=x代入双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得:
(b2-a2)x2=a2b2,
由题意可得b2-a2>0,
即有c2-2a2>0,
即为e2>2,即e>$\sqrt{2}$.
故选:B.
点评 本题考查双曲线的离心率的范围,注意运用联立直线方程和双曲线的方程,考查离心率公式的运用,以及运算能力,属于基础题.

练习册系列答案
相关题目
20.已知双曲线C:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线与直线y=-1所围成的三角形的面积为4,则双曲线C的离心率为( )
| A. | $\sqrt{15}$ | B. | $\frac{\sqrt{17}}{2}$ | C. | $\sqrt{17}$ | D. | $\frac{\sqrt{15}}{2}$ |
2.已知双曲线C:x2+2my2=1的两条渐近线互相垂直,则抛物线E:y=mx2的焦点坐标是( )
| A. | (0,1) | B. | (0,-1) | C. | (0,$\frac{1}{2}$) | D. | (0,-$\frac{1}{2}$) |
12.已知点(2,1)在双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线上,则C的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | $\frac{\sqrt{5}}{2}$ |
19.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为2x-y=0,则它的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
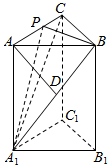 如图,在直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.
如图,在直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.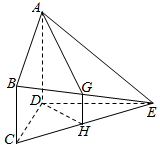 已知:如图所示,平面ABCD⊥平面CDE,BC∥AD,∠BCD=90°,CD⊥DE,AD=DC=DE=2BC=2,G,H分别是BE,CE的中点.
已知:如图所示,平面ABCD⊥平面CDE,BC∥AD,∠BCD=90°,CD⊥DE,AD=DC=DE=2BC=2,G,H分别是BE,CE的中点. 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.