题目内容
20.双曲线3x2-y2=75上一点P到它的一个焦点的距离等于12,那么点P到它的另一个焦点的距离等于22.分析 将双曲线的方程化为标准方程,可得a,b,c,由c+a=15,c-a=5,可得P,F1在y轴的同侧,设|PF1|=12,运用双曲线的定义,可得|PF2|=2或22,检验舍去2.
解答 解:双曲线3x2-y2=75即为
$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{75}$=1,即有a=5,b=5$\sqrt{3}$,c=10,
由c+a=15,c-a=5,可得P,F1在y轴的同侧,
设|PF1|=12,
由双曲线的定义可得||PF1|-|PF2||=2a=10,
即有|12-|PF2||=10,
解得|PF2|=2或22,
由|PF2|的最小值为c-a=5>2,
即有|PF2|=22,
故答案为:22.
点评 本题考查双曲线上的点到一焦点的距离的求法,注意运用双曲线的定义和焦半径的最小值,考查运算能力,属于基础题和易错题.

练习册系列答案
相关题目
14.下列式子正确的是( )
| A. | cos(-$\frac{π}{10}$)<cos(-$\frac{π}{9}$) | B. | tan$\frac{π}{6}$<tan$\frac{2}{7}$π | C. | sin$\frac{8}{7}$π>sin$\frac{π}{11}$ | D. | cos$\frac{2}{5}$π<cos$\frac{6}{5}$π |
8.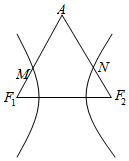 (普通中学做)如图,已知F1、F2为双曲线的两焦点,等边三角形AF1F2两边的中点M、N在双曲线上,则该双曲线的离心率为( )
(普通中学做)如图,已知F1、F2为双曲线的两焦点,等边三角形AF1F2两边的中点M、N在双曲线上,则该双曲线的离心率为( )
 (普通中学做)如图,已知F1、F2为双曲线的两焦点,等边三角形AF1F2两边的中点M、N在双曲线上,则该双曲线的离心率为( )
(普通中学做)如图,已知F1、F2为双曲线的两焦点,等边三角形AF1F2两边的中点M、N在双曲线上,则该双曲线的离心率为( )| A. | $\sqrt{3}$+1 | B. | $\sqrt{2}$+1 | C. | $\sqrt{5}$+1 | D. | $\sqrt{5}$-1 |
12.已知点(2,1)在双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线上,则C的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | $\frac{\sqrt{5}}{2}$ |
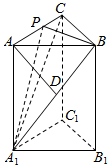 如图,在直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.
如图,在直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.