题目内容
10.焦点在x轴上,焦距为10,且与双曲线$\frac{{y}^{2}}{4}$-x2=1有相同渐近线的双曲线的标准方程是$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1.分析 设所求双曲线的标准方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),由题意可得2c=10,即c=5,求出已知双曲线的渐近线方程,可得a,b的方程组,解得a,b,即可得到所求双曲线的标准方程.
解答 解:设所求双曲线的标准方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),
由题意可得2c=10,即c=5,
由双曲线$\frac{{y}^{2}}{4}$-x2=1的渐近线方程为y=±2x,
可得$\frac{b}{a}$=2,又a2+b2=25,
解得a=$\sqrt{5}$,b=2$\sqrt{5}$,
即有双曲线的方程为$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1.
故答案为:$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1.
点评 本题考查双曲线的方程的求法,注意运用渐近线方程和a,b,c的关系,考查运算能力,属于基础题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
4.函数y=sin(x+$\frac{π}{4}$)图象的一条对称轴是( )
| A. | x轴 | B. | y轴 | C. | 直线x=$\frac{π}{4}$ | D. | 直线x=-$\frac{π}{4}$ |
2.已知双曲线C:x2+2my2=1的两条渐近线互相垂直,则抛物线E:y=mx2的焦点坐标是( )
| A. | (0,1) | B. | (0,-1) | C. | (0,$\frac{1}{2}$) | D. | (0,-$\frac{1}{2}$) |
19.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为2x-y=0,则它的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
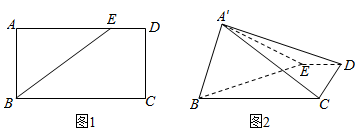
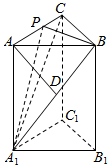 如图,在直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.
如图,在直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.