题目内容
8.已知函数f(x)=sinx+λcosx(λ∈R)的图象关于直线x=-$\frac{π}{4}$对称,把函数f(x)的图象上,每个点的横坐标扩大到原来的2倍,纵坐标不变,再将所得函数图象向右平移$\frac{π}{3}$个单位长度,得到函数g(x)的图象,则函数g(x)的一个对称中心是( )| A. | ($\frac{π}{6}$,0) | B. | ($\frac{π}{4}$,0) | C. | ($\frac{2π}{3}$,0) | D. | ($\frac{5π}{6}$,0) |
分析 根据函数的对称性利用特殊值法求出λ=-1,利用辅助角公式结合三角函数的图象变换关系求出g(x)的解析式,利用三角函数的对称性进行求解即可.
解答 解:若函数f(x)=sinx+λcosx(λ∈R)的图象关于直线x=-$\frac{π}{4}$对称,
则f(0)=f(-$\frac{π}{2}$),
即sin0+λcos0=sin(-$\frac{π}{2}$)+λcos(-$\frac{π}{2}$),
即λ=-1,
则f(x)=sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$),
函数f(x)的图象上,每个点的横坐标扩大到原来的2倍,纵坐标不变得到y=$\sqrt{2}$sin($\frac{1}{2}$x-$\frac{π}{4}$),
再将所得函数图象向右平移$\frac{π}{3}$个单位长度,得到函数g(x)的图象,即g(x)=$\sqrt{2}$sin[$\frac{1}{2}$(x-$\frac{π}{3}$)-$\frac{π}{4}$]=$\sqrt{2}$sin($\frac{1}{2}$x-$\frac{5π}{12}$),
由$\frac{1}{2}$x-$\frac{5π}{12}$=kπ,得x=2kπ+$\frac{5π}{6}$,k∈Z
当k=0时,函数的对称中心为($\frac{5π}{6}$,0),
故选:D.
点评 本题主要考查三角函数的图象和性质,利用三角函数的对称性以及三角函数的图象变换关系求出函数的解析式是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.若sinα=$\frac{1}{\sqrt{5}}$,sinβ=$\frac{1}{\sqrt{10}}$,且α、β∈(0,$\frac{π}{2}$),则α+β是( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$或$\frac{3π}{4}$ | D. | $\frac{π}{3}$ |
20.已知双曲线C:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线与直线y=-1所围成的三角形的面积为4,则双曲线C的离心率为( )
| A. | $\sqrt{15}$ | B. | $\frac{\sqrt{17}}{2}$ | C. | $\sqrt{17}$ | D. | $\frac{\sqrt{15}}{2}$ |
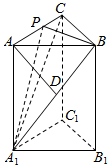 如图,在直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.
如图,在直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.