题目内容
已知双曲线的中心在坐标原点,焦点在x轴上,实轴长是虚轴长的2倍,且过点(2
,1),求双曲线的标准方程及离心率.
| 2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设出双曲线的标准方程,求出a、b的值,即可得出标准方程,从而求出它的离心率.
解答:
解:根据题意,设双曲线的标准方程是
-
=1,
则2a=4b①,
又双曲线过点(2
,1)
∴
-
=1②;
由①②联立,解得
a2=4,b2=1;
∴双曲线的标准方程是
-y2=1,
∴它的离心率是e=
=
=
.
| x2 |
| a2 |
| y2 |
| b2 |
则2a=4b①,
又双曲线过点(2
| 2 |
∴
| 8 |
| a2 |
| 1 |
| b2 |
由①②联立,解得
a2=4,b2=1;
∴双曲线的标准方程是
| x2 |
| 4 |
∴它的离心率是e=
| c |
| a |
| ||
| 2 |
| ||
| 2 |
点评:本题考查了用双曲线的标准方程与几何性质的应用问题,解题时应熟记双曲线的标准方程以及a、b、c与离心率e之间的关系,是基础题目.

练习册系列答案
相关题目
在正方体ABCD-A1B1C1D1中,平面A1BD与平面C1BD所成二面角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
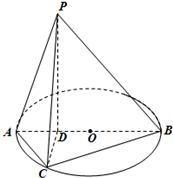 如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.
如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.