数列{an}满足a${\;} {n+2}^{2}$=an•an+4.且a3=2.a7=4.an＞0.则a11=8．题目和参考答案——青夏教育精英家教网——

题目内容

14．数列{a_n}满足a${\;}_{n+2}^{2}$=a_n•a_n+4，且a₃=2，a₇=4，a_n＞0，则a₁₁=8．

分析通过a${\;}_{n+2}^{2}$=a_n•a_n+4可知a_n，a_n+2，a_n+4构成等比数列，进而可知a₃，a₇，a₁₁构成等比数列，计算即得结论．

解答解：∵a${\;}_{n+2}^{2}$=a_n•a_n+4，
∴a_n，a_n+2，a_n+4构成等比数列，
又∵a₃=2，a₇=4，a_n＞0，
∴a₃，a₇，a₁₁构成等比数列，
∴a₁₁=$\frac{{{a}_{7}}^{2}}{{a}_{3}}$=$\frac{{4}^{2}}{2}$=8，
故答案为：8．

点评本题考查等比数列的通项，利用等比中项是解决本题的关键，注意解题方法的积累，属于基础题．

练习册系列答案

语文同步拓展阅读与训练系列答案

满分阅读系列答案

读写突破系列答案

语文读写双优训练系列答案

语文读本长春出版社系列答案

语篇初中英语阅读训练系列答案

优势阅读系列答案

优可英语系列答案

英语周计划系列答案

英语阅读理解天天练系列答案

相关题目

1．已知函数y=f（x+10）的定义域为[3，6]，则函数y=f（2x+1）+f（2x-1）的定义域为（　　）

[2，$\frac{7}{2}$]

[7，$\frac{15}{2}$]

5．三个数1，x，9成等比数列，则x=±3．

2．已知函数f（x）=2x³-3（a+1）x²+6ax+8．
（Ⅰ）当a=0时，求函数y=f（x）在（-1，f（-1））处的切线方程；
（Ⅱ）求函数f（x）的单调区间．

9．设定义域为[x₁，x₂]的函数y=f（x）的图象的为C．图象的两个端点分别为A、B，点O为坐标原点，点M是C上任意一点，向量$\overrightarrow{OA}$=（x₁，y₁），$\overrightarrow{OB}$=（x₂，y₂），且满足x=λx₁+（1-λ）x₂（0＜λ＜1），又设向量$\overrightarrow{ON}$=λ$\overrightarrow{OA}$+（1-λ）$\overrightarrow{OB}$．现定义函数y=f（x）在[x₁，x₂]上“可在标准下线性近似”是指|$\overrightarrow{MN}$|≤k恒成立，其中k＞0为常数．给出下列结论：
（1）A、B、N三点共线；
（2）直线MN的方向向量可以为$\overrightarrow{a}$=（0，1）；
（3）函数y=5x²在[0，1]上“可在标准下线性近似”；
（4）若函数y=x-$\frac{1}{x}$在[1，2]上“可在标准下线性近似”，则k≥$\frac{3}{2}$-$\sqrt{2}$．
其中所有正确结论的序号是（1），（2），（4）．

19．设数列{a_n}的前n项和为S_n，满足2S_n=a_n+1-2ⁿ⁺¹+1，n∈N^*，且a₁=1，设数列{b_n}满足b_n=a_n+2ⁿ．
（1）求证数列{b_n}为等比数列，并求出数列{a_n}的通项公式；
（2）若数列c_n=$\frac{6n-3}{{b}_{n}}$，T_n是数列{c_n}的前n项和，证明T_n＜3．

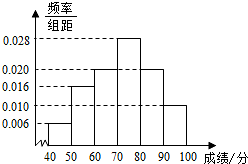新津中学高二15班学生参加“六校”联考，其数学成绩（已折合成百分制）的频率分布直方图如图所示，其中成绩分布敬意为[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]，现已知成绩落在[90，100]的有5人．
（Ⅰ）求该班参加“六校”联考的总人数；
（Ⅱ）根据频率分布直方图，估计该班此次数学成绩的平均分（可用中值代替各组数据的平均值）；
（Ⅲ）现要求从成绩在[40，50）和[90，100]的学生共选2人参加成绩分析会，求2人来自于同一分数段的概率．

3．已知a₁=1，a_n+1=$\frac{{{a}_{n}}^{2}+2}{2{a}_{n}-1}$，求a_n的通项公式．

4．在等比数列{a_n}中，相邻三项为a_n-1，a_n，a_n+1，则a_n=±$\sqrt{{a}_{n-1}{a}_{n+1}}$．