题目内容
3.已知a1=1,an+1=$\frac{{{a}_{n}}^{2}+2}{2{a}_{n}-1}$,求an的通项公式.分析 通过对an+1=$\frac{{{a}_{n}}^{2}+2}{2{a}_{n}-1}$变形可知an+1-2=$\frac{({a}_{n}-2)^{2}}{2{a}_{n}-1}$、an+1+1=$\frac{({a}_{n}+1)^{2}}{2{a}_{n}-1}$,两式相除、两边同时取对数整理可知lg$\frac{{a}_{n}-2}{{a}_{n}+1}$=2lg$\frac{{a}_{n-1}-2}{{a}_{n-1}+1}$、lg$\frac{{a}_{n-1}-2}{{a}_{n-1}+1}$=2lg$\frac{{a}_{n-2}-2}{{a}_{n-2}+1}$、…、lg$\frac{{a}_{2}-2}{{a}_{2}+1}$=2lg$\frac{{a}_{1}-2}{{a}_{1}+1}$,进而可知$\frac{{a}_{n}-2}{{a}_{n}+1}$=$(\frac{{a}_{1}-2}{{a}_{1}+1})^{{2}^{n-1}}$,计算即得结论.
解答 解:∵an+1=$\frac{{{a}_{n}}^{2}+2}{2{a}_{n}-1}$,
∴an+1-2=$\frac{{{a}_{n}}^{2}+2}{2{a}_{n}-1}$-2=$\frac{({a}_{n}-2)^{2}}{2{a}_{n}-1}$,
an+1+1=$\frac{{{a}_{n}}^{2}+2}{2{a}_{n}-1}$+1=$\frac{({a}_{n}+1)^{2}}{2{a}_{n}-1}$,
两式相除得:$\frac{{a}_{n+1}-2}{{a}_{n+1}+1}$=$(\frac{{a}_{n}-2}{{a}_{n}+1})^{2}$,
两边同时取对数得:lg$\frac{{a}_{n+1}-2}{{a}_{n+1}+1}$=2lg$\frac{{a}_{n}-2}{{a}_{n}+1}$,
∴lg$\frac{{a}_{n}-2}{{a}_{n}+1}$=2lg$\frac{{a}_{n-1}-2}{{a}_{n-1}+1}$,lg$\frac{{a}_{n-1}-2}{{a}_{n-1}+1}$=2lg$\frac{{a}_{n-2}-2}{{a}_{n-2}+1}$,…,lg$\frac{{a}_{2}-2}{{a}_{2}+1}$=2lg$\frac{{a}_{1}-2}{{a}_{1}+1}$,
∴lg$\frac{{a}_{n}-2}{{a}_{n}+1}$=2n-1lg$\frac{{a}_{1}-2}{{a}_{1}+1}$,即$\frac{{a}_{n}-2}{{a}_{n}+1}$=$(\frac{{a}_{1}-2}{{a}_{1}+1})^{{2}^{n-1}}$,
又∵$\frac{{a}_{1}-2}{{a}_{1}+1}$=$\frac{1-2}{1+1}$=-$\frac{1}{2}$,
∴$\frac{{a}_{n}-2}{{a}_{n}+1}$=$(-\frac{1}{2})^{{2}^{n-1}}$,
整理得:an=2+3•$\frac{(-\frac{1}{2})^{{2}^{n-1}}}{1-(-\frac{1}{2})^{{2}^{n-1}}}$.
点评 本题考查数列是的通项,考查运算求解能力,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于难题.

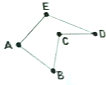 如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )
如图,折五边形ABCDE中,若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯(每种颜色灯都不少于5个),每处装上一个信号灯,求使得相邻顶点所放灯的颜色不同的概率是( )| A. | $\frac{10}{81}$ | B. | $\frac{1}{9}$ | C. | $\frac{8}{81}$ | D. | $\frac{7}{81}$ |