题目内容
9.设定义域为[x1,x2]的函数y=f(x)的图象的为C.图象的两个端点分别为A、B,点O为坐标原点,点M是C上任意一点,向量$\overrightarrow{OA}$=(x1,y1),$\overrightarrow{OB}$=(x2,y2),且满足x=λx1+(1-λ)x2(0<λ<1),又设向量$\overrightarrow{ON}$=λ$\overrightarrow{OA}$+(1-λ)$\overrightarrow{OB}$.现定义函数y=f(x)在[x1,x2]上“可在标准下线性近似”是指|$\overrightarrow{MN}$|≤k恒成立,其中k>0为常数.给出下列结论:(1)A、B、N三点共线;
(2)直线MN的方向向量可以为$\overrightarrow{a}$=(0,1);
(3)函数y=5x2在[0,1]上“可在标准下线性近似”;
(4)若函数y=x-$\frac{1}{x}$在[1,2]上“可在标准下线性近似”,则k≥$\frac{3}{2}$-$\sqrt{2}$.
其中所有正确结论的序号是(1),(2),(4).
分析 对于(1)根据向量共线即可判断,对于(2)说明M,N的横坐标相同即可.
对于(3),(4)先得出M、N横坐标相等,再将恒成立问题转化为求函数的最值问题.
解答 解:由向量$\overrightarrow{ON}$=λ$\overrightarrow{OA}$+(1-λ)$\overrightarrow{OB}$,得$\overrightarrow{ON}-\overrightarrow{OB}$=λ($\overrightarrow{OA}$-$\overrightarrow{OB}$),即$\overrightarrow{BN}$=λ$\overrightarrow{BA}$,故(1)成立;
∵向量$\overrightarrow{OA}$=(x1,y1),$\overrightarrow{OB}$=(x2,y2),且满足x=λx1+(1-λ)x2(0<λ<1),
∴向量的横坐标为λx1+(1-λ)x2(0<λ<1),
∵$\overrightarrow{OM}$=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),
∴MN∥y轴,
∴直线MN的方向向量可以为$\overrightarrow{a}$=(0,1),故(2)成立,
对于函数y=5x2在[0,1]上,易得A(0,0),B(1,5),
所以M(1-λ,5(1-λ)2),N(1-λ,5(1-λ)),
从而|$\overrightarrow{MN}$|=$\sqrt{{5}^{2}(1-λ)^{2}-(1-λ)^{2}}$=$\sqrt{25[(λ-\frac{1}{2})^{2}+\frac{1}{4}]^{2}}$≤$\frac{5}{4}$,
故函数y=5x2在[0,1]上可在标准下线性近似”,(3)不成立,
对于函数y=x+$\frac{1}{x}$在[1,2]上,易得A(1,0),B=(2,$\frac{3}{2}$),
∴直线AB方程为y=$\frac{3}{2}$(x-1)
∴|$\overrightarrow{MN}$|=y1-y2=x-$\frac{1}{x}$-$\frac{3}{2}$(x-1)=$\frac{3}{2}$-($\frac{x}{2}$+$\frac{1}{x}$)≤$\frac{3}{2}$$-\sqrt{2}$(当且仅当x=$\sqrt{2}$时,取等号)
∵x∈[1,2],
∴x=$\sqrt{2}$时,
|$\overrightarrow{MN}$|的最大值为$\frac{3}{2}$$-\sqrt{2}$,
∴则k≥$\frac{3}{2}$-$\sqrt{2}$.故(4)正确.
故答案为:(1)(2)(4)
点评 本题考查向量知识的运用,考查基本不等式的运用,解答的关键是将已知条件进行转化,同时应注意恒成立问题的处理策略.

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案| A. | ($\frac{π}{3}$,0) | B. | ($\frac{π}{6}$,0) | C. | (-$\frac{π}{3}$,0) | D. | (-$\frac{π}{6}$,0) |
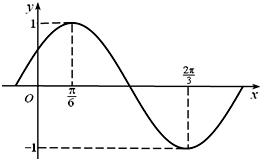 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.