题目内容
4．在等比数列{an}中，相邻三项为an-1，an，an+1，则an=±$\sqrt{{a}_{n-1}{a}_{n+1}}$．分析 由等比数列的性质可得an2=an-1an+1，可得答案．
解答 解：设等比数列{an}的公比为q，
则an-1=$\frac{{a}_{n}}{q}$，an+1=anq，
∴an2=an-1an+1，
∴an=±$\sqrt{{a}_{n-1}{a}_{n+1}}$
故答案为：±$\sqrt{{a}_{n-1}{a}_{n+1}}$
点评 本题考查等比数列的通项公式和性质，属基础题．
练习册系列答案
相关题目
15．
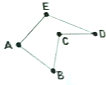如图，折五边形ABCDE中，若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯（每种颜色灯都不少于5个），每处装上一个信号灯，求使得相邻顶点所放灯的颜色不同的概率是（ ）
如图，折五边形ABCDE中，若在顶点A、B、C、D、E处装上红、黄、绿三种颜色信号灯（每种颜色灯都不少于5个），每处装上一个信号灯，求使得相邻顶点所放灯的颜色不同的概率是（ ）| A． | $\frac{10}{81}$ | B． | $\frac{1}{9}$ | C． | $\frac{8}{81}$ | D． | $\frac{7}{81}$ |
19．如果把函数y=$\frac{1}{4}$sin2x的图象按向量$\overrightarrow{v}$平移，就可以得到函数y=$\frac{1}{4}$sin（2x-$\frac{π}{3}$）的图象，那么向量$\overrightarrow{v}$的坐标是（ ）
| A． | （$\frac{π}{3}$，0） | B． | （$\frac{π}{6}$，0） | C． | （-$\frac{π}{3}$，0） | D． | （-$\frac{π}{6}$，0） |
16．从一群游戏的孩子中随机抽出k人，每人分一个苹果，让他们返回继续游戏．过一会儿，再从中任取m人，发现其中有n个孩子曾分过苹果，估计参加游戏的孩子的人数为（ ）
| A． | $\frac{kn}{m}$ | B． | $\frac{km}{n}$ | C． | k+m-n | D． | k+m+n |