题目内容
已知:等差数列{an}的前n项和为Sn,若公差d=-2,S20=0.
(Ⅰ)求通项an及Sn;
(Ⅱ)设{bn-an}是首项为1,公比为3的等比数列,求数列{bn}的通项公式及其前n项和Tn.
(Ⅰ)求通项an及Sn;
(Ⅱ)设{bn-an}是首项为1,公比为3的等比数列,求数列{bn}的通项公式及其前n项和Tn.
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(Ⅰ)由S20=0,S20=20a1+
d=0,求出d,a1即可求出通项an及Sn;
(Ⅱ)求出bn-an=3n-1,得出bn=3n-1+an=3n-1-2n+21,转化为等比等差数列求和公式求解.
| 20×19 |
| 2 |
(Ⅱ)求出bn-an=3n-1,得出bn=3n-1+an=3n-1-2n+21,转化为等比等差数列求和公式求解.
解答:
解:(Ⅰ)由S20=0,S20=20a1+
d=0,
2a1+19d=0,
d=2,a1=19,
an=a1+(n-1)d=19-2(n-1)=-2n+21,
Sn=na1+
d=19n-n(n-1)=-n2+20n,
(Ⅱ)bn-an=3n-1,
∴bn=3n-1+an=3n-1-2n+21,
Tn=Sn+(1+3+32+33+…+3n-1)=-n2+20n+
.
| 20×19 |
| 2 |
2a1+19d=0,
d=2,a1=19,
an=a1+(n-1)d=19-2(n-1)=-2n+21,
Sn=na1+
| n(n-1) |
| 2 |
(Ⅱ)bn-an=3n-1,
∴bn=3n-1+an=3n-1-2n+21,
Tn=Sn+(1+3+32+33+…+3n-1)=-n2+20n+
| 3n-1 |
| 2 |
点评:本题考察了等差等比数列的性质,公式,运用求解通项,前n项的和,属于中档题.

练习册系列答案
相关题目
已知A,B,C三点共线,O为直径AB外的任一点,满足
=x
+y
,则x2+y的最小值等于( )
| OC |
| OA |
| OB |
A、
| ||
| B、1 | ||
C、
| ||
D、
|
命题p:“?x∈R,2x-1>0”,命题q:“函数f(x)=x-
是奇函数”,则下列命题正确的是( )
| 1 |
| x |
| A、命题“p∧q”是真命题 |
| B、命题“(¬p)∧q”是真命题 |
| C、命题“p∧(¬q)”是真命题 |
| D、命题“(¬p)∧(¬q)”是真命题 |

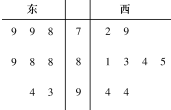 某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.