题目内容
已知函数f(x)=
x2-alnx
(1)若曲线y=f(x)在x=1处的切线与直线2x-y+1=0平行,求a的值;
(2)求函数f(x)的单调区间;
(3)对任意的n∈N*,求证:
n2>lnn.
| 1 |
| 2 |
(1)若曲线y=f(x)在x=1处的切线与直线2x-y+1=0平行,求a的值;
(2)求函数f(x)的单调区间;
(3)对任意的n∈N*,求证:
| 1 |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(1)由题意可得f′(1)=2,解出即可;
(2)分a≤0,a>0两种情况讨论,在定义域内解不等式f′(x)>0,f′(x)<0即可;
(3)取a=1,由(2)可得f(x)≥f(1)=
,由此可得结论;
(2)分a≤0,a>0两种情况讨论,在定义域内解不等式f′(x)>0,f′(x)<0即可;
(3)取a=1,由(2)可得f(x)≥f(1)=
| 1 |
| 2 |
解答:
解:(1)f′(x)=x-
,
由题意知y=f(x)在x=1处的切线斜率为2,即f′(1)=2,
∴1-a=2,解得a=-1;
(2)f(x)的定义域为(0,+∞),
f′(x)=x-
=
,
当a≤0时,f′(x)>0,f(x)在(0,+∞)上单调递增;
当a>0时,由f′(x)<0,得0<x<
;由f′(x)>0,得x>
.
∴当a≤0时,f(x)的递增区间为(0,+∞);当a>0时,f(x)的递减区间是(0,
],递增区间是[
,+∞).
(3)取a=1,由(2)知,f(x)=
x2-lnx在[1,+∞)上单调递增,
∴f(x)≥f(1)=
,
∴
x2-lnx≥
,
x2≥lnx+
,
∴对任意的n∈N*,
n2≥lnn+
>lnn.
| a |
| x |
由题意知y=f(x)在x=1处的切线斜率为2,即f′(1)=2,
∴1-a=2,解得a=-1;
(2)f(x)的定义域为(0,+∞),
f′(x)=x-
| a |
| x |
| x2-a |
| x |
当a≤0时,f′(x)>0,f(x)在(0,+∞)上单调递增;
当a>0时,由f′(x)<0,得0<x<
| a |
| a |
∴当a≤0时,f(x)的递增区间为(0,+∞);当a>0时,f(x)的递减区间是(0,
| a |
| a |
(3)取a=1,由(2)知,f(x)=
| 1 |
| 2 |
∴f(x)≥f(1)=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴对任意的n∈N*,
| 1 |
| 2 |
| 1 |
| 2 |
点评:该题考查导数的几何意义、利用导数研究函数的单调性、最值,考查学生分析解决问题的能力,注意:求单调区间要在定义域内进行.

练习册系列答案
相关题目
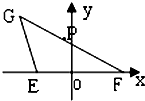 已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,|
已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,|