题目内容
 已知函数f(x)=lnx,g(x)=
已知函数f(x)=lnx,g(x)=| 1 |
| 2 |
(1)若曲线y=f(x)-g(x)在x=1与x=
| 1 |
| 2 |
(2)若函数y=f(x)-g(x)在区间(
| 1 |
| 3 |
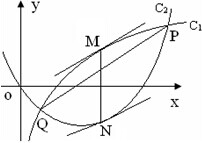
(3)设函数f(x)的图象C1与函数g(x)的图象C2交于P,Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:综合题,导数的概念及应用
分析:(1)求函数y=f(x)-g(x)的导数,根据在x=1与x=
处的切线相互平行,得到导数相同,建立方程即可求a的值及切线斜率.
(2)要使函数y=f(x)-g(x)在区间(
,1)上单调递减,只要y'≤0恒成立即可求a的取值范围.
(3)利用反证法证明结论即可.
| 1 |
| 2 |
(2)要使函数y=f(x)-g(x)在区间(
| 1 |
| 3 |
(3)利用反证法证明结论即可.
解答:
(1)解:y=f(x)-g(x)=lnx-
ax2+2x,记h(x)=lnx-
ax2+2x,
则h′(x)=
-ax+2…(2分)
∵依题意h(x)在x=1与x=
处的切线互相平行,
∴h′(1)=h′(
),即-a+3=-
+4,解得a=-2…(3分)
此时切线斜率k=h'(1)=5…(4分)
(2)解:∵函数y=f(x)-g(x)在区间(
,1)上单调递减,
∴h′(x)≤0在区间(
,1)上恒成立;…(5分)
即
-ax+2≤0,即a≥
+
在区间(
,1)上恒成立;…(6分)
∴a≥(
+
)max,
∵x∈(
,1),∴
∈(1,3),
∴
+
=(
+1)2-1≤15,
∴a≥15,
即a的取值范围是[15,+∞).…(8分)
(3)证明:f′(x)=
,g′(x)=ax-2,假设C1在点M处的切线与C2在点N处的切线平行,
设点P、Q的坐标分别是(x1,y1),(x2,y2),x1>x2,>0,
则存在a使得f′(
)=g′(
),
即
=
(x1+x2)-2,…(9分)
∴
=
(x1+x2)(x1-x2)-2(x1-x2)=y1-y2=lnx1-lnx2=ln
不妨设
=t>1…(12分)
则方程
=lnt存在大于1的实根,
设φ(t)=
-lnt,则φ′(t)=
<0,
∴φ(t)在(1,+∞)单调递减,
∴φ(t)<φ(1)=0这与存在t>1使得φ(t)=0矛盾.
∴C1在点M处的切线与C2在点N处的切线不可能平行.…(14分)
| 1 |
| 2 |
| 1 |
| 2 |
则h′(x)=
| 1 |
| x |
∵依题意h(x)在x=1与x=
| 1 |
| 2 |
∴h′(1)=h′(
| 1 |
| 2 |
| a |
| 2 |
此时切线斜率k=h'(1)=5…(4分)
(2)解:∵函数y=f(x)-g(x)在区间(
| 1 |
| 3 |
∴h′(x)≤0在区间(
| 1 |
| 3 |
即
| 1 |
| x |
| 1 |
| x2 |
| 2 |
| x |
| 1 |
| 3 |
∴a≥(
| 1 |
| x2 |
| 2 |
| x |
∵x∈(
| 1 |
| 3 |
| 1 |
| x |
∴
| 1 |
| x2 |
| 2 |
| x |
| 1 |
| x |
∴a≥15,
即a的取值范围是[15,+∞).…(8分)
(3)证明:f′(x)=
| 1 |
| x |
设点P、Q的坐标分别是(x1,y1),(x2,y2),x1>x2,>0,
则存在a使得f′(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
即
| 2 |
| x1+x2 |
| a |
| 2 |
∴
| 2(x1-x2) |
| x1+x2 |
| a |
| 2 |
| x1 |
| x2 |
不妨设
| x1 |
| x2 |
则方程
| 2(t-1) |
| t+1 |
设φ(t)=
| 2(t-1) |
| t+1 |
| -(t-1)2 |
| t(t+1) |
∴φ(t)在(1,+∞)单调递减,
∴φ(t)<φ(1)=0这与存在t>1使得φ(t)=0矛盾.
∴C1在点M处的切线与C2在点N处的切线不可能平行.…(14分)
点评:本题主要考查导数的几何意义,考查导数是运算,以及利用导数研究函数的性质,综合性较强,运算量较大,考查学生的运算能力.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
在平面直角坐标系中,记由点A(0,1),B(4,2),C(2,6)围成的三角形区域(含边界)为D,P(x,y)为区域D上的点,则
最大值与最小值的和为( )
| (x-2)2+(y-2)2 |
A、
| ||||||||
B、
| ||||||||
| C、4 | ||||||||
D、
|
 如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD.AB=AD=
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD.AB=AD=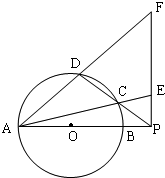 如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P做AP的垂线,交直线AC于点E,交直线AD于点F.
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P做AP的垂线,交直线AC于点E,交直线AD于点F.