题目内容
若θ∈[
,
],sin2θ=
,则cosθ=( )
| π |
| 4 |
| π |
| 2 |
3
| ||
| 8 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
考点:二倍角的正弦
专题:三角函数的求值
分析:根据三角函数的倍角公式,进行化简求解即可.
解答:
解:∵θ∈[
,
],
∴2θ∈[
,π],
则cos2θ=-
=-
,
∵cos2θ=2cos2θ-1=-
,
∴cos2θ=
,即cosθ=
,
故选:C
| π |
| 4 |
| π |
| 2 |
∴2θ∈[
| π |
| 2 |
则cos2θ=-
1-(
|
| 1 |
| 8 |
∵cos2θ=2cos2θ-1=-
| 1 |
| 8 |
∴cos2θ=
| 7 |
| 16 |
| ||
| 4 |
故选:C
点评:本题主要考查三角函数的化简和求值,利用三角函数的倍角公式是解决本题的关键,考查学生的计算能力.

练习册系列答案
相关题目
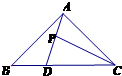 如图,在直角△ABC中,|
如图,在直角△ABC中,|| AB |
| AC |
| DC |
| BD |
| AP |
| CP |
A、[0,
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
已知a,b,c为△ABC的三边,若b2+c2-a2=bc,则
的取值范围是( )
| b+c |
| a |
| A、(1,2] | ||
B、(1,
| ||
C、[
| ||
D、(
|
设复数z=-3i+1,则z的共轭复数在复平面内对应的点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
执行如图所示的程序框图,则输出的结果是( )


| A、128 | B、127 |
| C、64 | D、63 |
在平面直角坐标系中,记由点A(0,1),B(4,2),C(2,6)围成的三角形区域(含边界)为D,P(x,y)为区域D上的点,则
最大值与最小值的和为( )
| (x-2)2+(y-2)2 |
A、
| ||||||||
B、
| ||||||||
| C、4 | ||||||||
D、
|
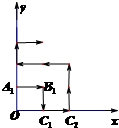 某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点A1(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么
某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点A1(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么