题目内容
3.已知定义域为R的奇函数f(x)=x|x+m|.(1)求出m的值,并解不等式f(x)≥x;
(2)对任意x1,x2∈[1,1+a],总有|f(x1)-f(x2)|≤2,求实数a的取值范围.
分析 由题意先求出m,代入求函数解析式;
(1)由x|x|≥x可得$\left\{\begin{array}{l}{x}^{\;}≥0\\{x}^{2}≥x\end{array}\right.$或$\left\{\begin{array}{l}{x}^{\;}<0\\-{x}^{2}≥x\end{array}\right.$,从而解不等式;
(2)由f(x)=$\left\{\begin{array}{l}{x}^{2},x≥0\\-{x}^{2},x<0\end{array}\right.$,可知f(x)在R上单调递增,从而化对任意x1,x2∈[1,1+a],总有|f(x1)-f(x2)|≤2为f(1+a)-f(1)≤2,从而解得.
解答 解:∵f(x)=x|x+m|是定义域为R的奇函数,
∴m=0,
∴f(x)=x|x|;
(1)由x|x|≥x得,
$\left\{\begin{array}{l}{x}^{\;}≥0\\{x}^{2}≥x\end{array}\right.$或$\left\{\begin{array}{l}{x}^{\;}<0\\-{x}^{2}≥x\end{array}\right.$;
解得,x≥1或-1≤x≤0,
故不等式的解集为{x|x≥1或-1≤x≤0};
(2)f(x)=$\left\{\begin{array}{l}{x}^{2},x≥0\\-{x}^{2},x<0\end{array}\right.$,
则f(x)在R上单调递增,
∴f(x)在[1,1+a]上单调递增,
∴f(1+a)-f(1)≤2,
即(1+a)|1+a|-1≤2,
又∵1+a>1,
∴0<a≤$\sqrt{3}$-1.
点评 本题考查了分段函数的应用,二次函数的性质,函数的奇偶性的应用,属于中档题.

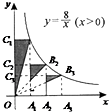 如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$.
如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$. 20名学生某次数学考试成绩(单位:分)的频率分布直方图如下:
20名学生某次数学考试成绩(单位:分)的频率分布直方图如下: