题目内容
18．（1）求函数$f（x）=\frac{{\sqrt{4-x}}}{x-1}$的定义域；（2）求函数y=-x2-6x+7的值域．
分析 （1）由根式内部的代数式大于等于0，分式的分母不为0联立不等式组得答案；
（2）直接求出二次函数顶点的纵坐标得到函数y=-x2-6x+7的值域．
解答 解：（1）由原函数得$\left\{{\begin{array}{l}{4-x≥0}\\{x-1≠0}\end{array}}\right.$，解之得x≤4且x≠1，
故所求函数的定义域为（-∞，1）∪（1，4]；
（2）由原函数知函数图象开口向下，
∴$y≤\frac{{4×（{-1}）×7-{{（{-6}）}^2}}}{{4×（{-1}）}}=16$，
故所求函数的值域为（-∞，16]．
点评 本题考查函数的定义域及值域的求法，训练了二次函数最大值的求法，是基础题．
练习册系列答案
相关题目
8．
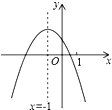二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：
①4ac-b2＜0；
②4a+c＜2b；
③3b+2c＜0；
④m（am+b）+b＜a（m≠-1），
其中正确结论的个数是（ ）
二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①4ac-b2＜0；
②4a+c＜2b；
③3b+2c＜0；
④m（am+b）+b＜a（m≠-1），
其中正确结论的个数是（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
13．在等差数列{an}中，a1=2，a2=$\frac{5}{2}$，则a4的值为（ ）
| A． | $\frac{7}{2}$ | B． | 4 | C． | $\frac{9}{2}$ | D． | $\frac{1}{2}$ |
10．已知角α的终边经过点（-3，4），则$sin（{α+\frac{π}{4}}）$的值（ ）
| A． | $\frac{\sqrt{2}}{5}$ | B． | -$\frac{\sqrt{2}}{5}$ | C． | $\frac{\sqrt{2}}{10}$ | D． | -$\frac{\sqrt{2}}{10}$ |
7．根据历年气象资料统计，蚌埠地区五月份刮东风的概率是$\frac{4}{15}$，既刮东风又下雨的概率是$\frac{7}{30}$，那么在“五月份刮东风”的条件下，蚌埠地区五月份下雨的概率是（ ）
| A． | $\frac{1}{30}$ | B． | $\frac{1}{2}$ | C． | $\frac{56}{900}$ | D． | $\frac{7}{8}$ |
8．已知集合A={x||x-1|＞x-1}，B={y|y=lnx}，则A∩B=（ ）
| A． | {x|0＜x＜1} | B． | {x|x＜1} | C． | {x|0＜x≤1} | D． | {x|x≤1} |