题目内容
13.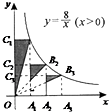 如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$.
如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$.
分析 根据反比例函数的比例系数k的几何意义得到第1个阴影三角形的面积=4,由于第2个阴影三角形与三角形OB2C2相似,根据相似得性质得则第2个阴影三角形的面积=$\frac{1}{4}$S△OB2C2=($\frac{1}{2}$)2×$\frac{1}{2}$×8=$\frac{4}{4}$,同理可得第3个阴影三角形的面积,即可求出阴影部分的面积之和.
解答 解:第1个阴影三角形的面积=$\frac{1}{2}$×8=4,
第2个阴影三角形的面积=$\frac{1}{4}$S△OB2C2=($\frac{1}{2}$)2×$\frac{1}{2}$×8=$\frac{4}{4}$,
第3个阴影三角形的面积=$\frac{1}{9}$S△OB3C3=($\frac{1}{3}$)2×$\frac{1}{2}$×8=$\frac{4}{9}$,
所以图中阴影部分的面积之和为4(1+$\frac{1}{4}$+$\frac{1}{9}$)=$\frac{49}{9}$.
故答案为:$\frac{49}{9}$.
点评 本题考查了反比例函数的比例系数k的几何意义,考查了相似三角形面积的比等于相似比的平方,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R)
(Ⅰ)证明:无论m取什么实数,l与圆恒交于两点;
(Ⅱ)求直线被圆C截得的弦长最小时l的方程.
(Ⅰ)证明:无论m取什么实数,l与圆恒交于两点;
(Ⅱ)求直线被圆C截得的弦长最小时l的方程.
1.过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于A,B两点,交其准线于点C,若|AF|=6,且|BC|=2|BF|,则此抛物线方程为( )
| A. | y2=4x | B. | y2=6x | C. | y2=8x | D. | y2=9x |
8.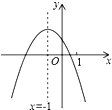 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①4ac-b2<0;
②4a+c<2b;
③3b+2c<0;
④m(am+b)+b<a(m≠-1),
其中正确结论的个数是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;
②4a+c<2b;
③3b+2c<0;
④m(am+b)+b<a(m≠-1),
其中正确结论的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
18.设y=f(x)存在导数,且满足$\lim_{△→0}\frac{f(1-△x)-f(1)}{△x}$=1,则曲线y=f(x)在(1,f(1))处的切线倾斜角为( )
| A. | 30° | B. | 135° | C. | 45° | D. | 120° |