Question

13．$f（x）=\left\{{\begin{array}{l}{2x-2，（x≤1）}\\{{x^2}-4x+3，（x＞1）}\end{array}}\right.$的图象和g（x）=log₂x的图象的交点个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 在同一坐标系中画出$f（x）=\left\{{\begin{array}{l}{2x-2，（x≤1）}\\{{x^2}-4x+3，（x＞1）}\end{array}}\right.$的图象和g（x）=log₂x的图象，数形结合，可得答案．

解答 解：$f（x）=\left\{{\begin{array}{l}{2x-2，（x≤1）}\\{{x^2}-4x+3，（x＞1）}\end{array}}\right.$的图象和g（x）=log₂x的图象如下图所示：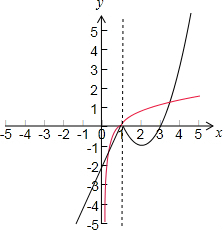

由图可得：两个函数图象共有3个交点，
故选：C

点评 本题考查的知识点是分段函数的应用，对数函数的图象和性质，函数交点个数的判断，难度中档．