题目内容
(本小题共14分)
正方体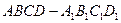 的棱长为
的棱长为 ,
, 是
是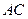 与
与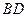 的交点,
的交点,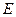 是
是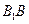 上一点,且
上一点,且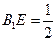 .(Ⅰ)求证:
.(Ⅰ)求证: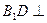 平面
平面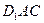 ;
;
(Ⅱ)求异面直线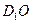 与
与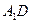 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求直线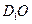 与平面
与平面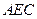 所成角的正弦值.
所成角的正弦值.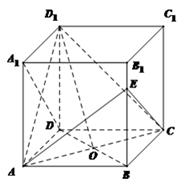
正方体
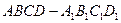 的棱长为
的棱长为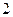 ,
,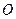 是
是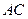 与
与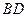 的交点,
的交点,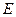 是
是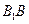 上一点,且
上一点,且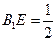 .(Ⅰ)求证:
.(Ⅰ)求证: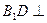 平面
平面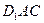 ;
;(Ⅱ)求异面直线
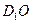 与
与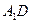 所成角的余弦值;
所成角的余弦值;(Ⅲ)求直线
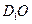 与平面
与平面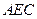 所成角的正弦值.
所成角的正弦值.
(Ⅰ)见解析(Ⅱ) (Ⅲ)
(Ⅲ)
 (Ⅲ)
(Ⅲ)
(Ⅰ)如图,以 为原点建立空间直
为原点建立空间直 角坐标系
角坐标系 .
.
则 ,
, ,
, ,
, ,
,
∴ ,
, ,
, .
.

 ,
,

又 与
与 交于
交于 点
点
 ,
,
∴ 平面
平面 .------------4分
.------------4分
(Ⅱ)设 与
与 所成的角为
所成的角为 .
.
 ,
, ,
, .
.
∴ ,
,
 .
.
∴ .
.
所求异面直线 与
与 所成角的余弦值为
所成角的余弦值为 .---------------9分
.---------------9分
(Ⅲ)设平面 与直线
与直线 所成的角为
所成的角为 .
.
设平面 的法向量为
的法向量为 .
.
 ,
, ,
, ,
, ,
, .
.

令 ,则
,则

 .
.

 .
.
所求平 面
面 与直线
与直线 所成角的正弦值为
所成角的正弦值为 .--------------------14分
.--------------------14分
 为原点建立空间直
为原点建立空间直 角坐标系
角坐标系 .
.则
 ,
, ,
, ,
, ,
,
∴
 ,
, ,
, .
.
 ,
,
又
 与
与 交于
交于 点
点 ,
,
∴
 平面
平面 .------------4分
.------------4分(Ⅱ)设
 与
与 所成的角为
所成的角为 .
. ,
, ,
, .
.∴
 ,
, .
.∴
 .
.所求异面直线
 与
与 所成角的余弦值为
所成角的余弦值为 .---------------9分
.---------------9分
(Ⅲ)设平面
 与直线
与直线 所成的角为
所成的角为 .
.设平面
 的法向量为
的法向量为 .
. ,
, ,
, ,
, ,
, .
.
令
 ,则
,则

 .
.
 .
.所求平
 面
面 与直线
与直线 所成角的正弦值为
所成角的正弦值为 .--------------------14分
.--------------------14分
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 平面ACB1)作垂直于D1B的平面分别交过D1的三条棱于E、F、G.
平面ACB1)作垂直于D1B的平面分别交过D1的三条棱于E、F、G.
 的底面为直角梯形,
的底面为直角梯形, ,
, 底面
底面 ,且
,且 ,
, ,
, 是
是 的中点.
的中点.
 面
面 ;
; 与
与 的正弦值.
的正弦值. 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱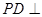 底面ABCD,
底面ABCD,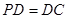 ,E是PC的中点,作
,E是PC的中点,作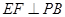 交PB于点F.
交PB于点F.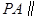 平面
平面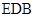 ;
;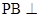 平面EFD;
平面EFD; 的大小.
的大小.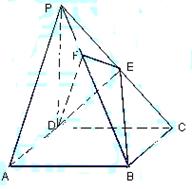
 的正方体
的正方体 中,
中, 、
、 分别是
分别是 、
、 的中点,求点
的中点,求点 到截面
到截面 的距离 .
的距离 . 的长方体被截面
的长方体被截面 所截而得到的,其中
所截而得到的,其中 .
. ;
; 到平面
到平面
 ,则
,则 的取值范围是( )
的取值范围是( )





 的面积。
的面积。 ,
, ,
, 是平面
是平面 内的三点,设向量
内的三点,设向量 ,且
,且 ,则
,则 ________________。
________________。