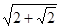题目内容
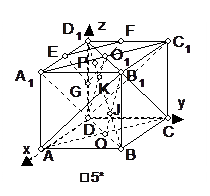
如图5:正方体ABCD-A1B1C1D1,过线段BD1上一点P(P 平面ACB1)作垂直于D1B的平面分别交过D1的三条棱于E、F、G.
平面ACB1)作垂直于D1B的平面分别交过D1的三条棱于E、F、G.
(1)求证:平面EFG∥平面A CB1,并判断三角形类型;
(2)若正方体棱长为a,求△EFG的最大面积,并求此时EF与B1C的距离.
 平面ACB1)作垂直于D1B的平面分别交过D1的三条棱于E、F、G.
平面ACB1)作垂直于D1B的平面分别交过D1的三条棱于E、F、G.(1)求证:平面EFG∥平面A CB1,并判断三角形类型;
(2)若正方体棱长为a,求△EFG的最大面积,并求此时EF与B1C的距离.

(1)见解析(2)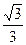 ·a
·a
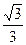 ·a
·a(证明(1)用纯粹的几何方法要辗转证明EF∥AC,EG∥B1C,FG∥AB1来证明,而我们借用向量法使问题代数化,运算简洁,思路简单明了.)
(1)分析:要证平面EFG平面ACB1,由题设知只要证BD1垂直平面ACB1即可.
证明:以D为坐标原点,建立空间直角坐标系,如图5,不妨设正方体棱长为a,则A(a,0,0),B(a,a,0),C(0,a,0),D1(0,0,a),B1(a,a,a),E(xE,0,a),F(0,yF,a),G(0,0,zG).
∴ =(-a,-a,a),
=(-a,-a,a),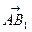 =(0,a,a),
=(0,a,a),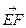 (-xE,yF,0),
(-xE,yF,0),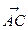 =(-a,a,0),
=(-a,a,0),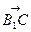 =(-a,0,-a),
=(-a,0,-a),
∵ ·
·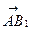 =(-a,-a,a)·(0,a,a)=0,
=(-a,-a,a)·(0,a,a)=0,
∴ ⊥
⊥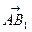 ,
,
同理 ⊥
⊥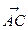 ,
,
而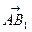 与
与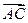 不共线且相交于点A,
不共线且相交于点A,
∴ ⊥平面ACB1,又已知
⊥平面ACB1,又已知 ⊥平面EFG,
⊥平面EFG,
∴平面EFG∥平面ACB1;
又因为 ⊥平面EFG,所以
⊥平面EFG,所以 ⊥
⊥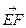 ,
,
则 ·
·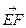 =0,
=0,
即 (-a,-a,a)·(-xE,yF,0)=0,
化简得 xE-yF=0;
同理 xE-zG="0, " yF-zG=0,
易得
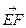
 =
=
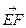
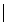 =
=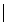
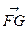
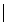 ,
,
∴ △EFG为正三角形.
(2)解:因为△EFG是正三角形,显然当△EFG与△A1C1D重合时,△EFG的边最长,其面积也最大,此时,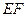 =A1C1=
=A1C1=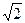 ·a,
·a,
∴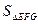 =
=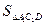
=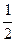
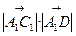 ·sin600
·sin600
=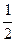 (
(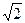 ·a)2·
·a)2·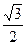
=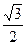 ·a2 .
·a2 .
此时EF与B1C的距离即为A1C1与B1C的距离,由于两异面直线所在平面平行,所求距离转化为求点B1到平面A1C1D的距离,记A1C1与B1D1交于点O1,作O1H∥D1B并交BB1于点H,则O1H⊥平面A1C1D,垂足为O1,则O1(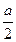 ,
,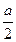 ,a),H(a,a,
,a),H(a,a,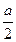 ),而
),而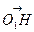 作为平面A1C1D的法向量,
作为平面A1C1D的法向量,
所以异面直线EF与B1C的距离设为d是
d =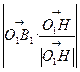 =
=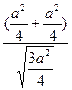 =
=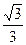 ·a.
·a.
(证明(2)时一般要找到求这两平面距离的两点,如图5*,而这两点为K与J,在立体图形中较难确定,且较难想到通过作辅助线DO1,OB1来得到,加上在如此复杂的空间图形中容易思维混乱,但只要借助平面法向量求线段的射影长度的思想,结合题设,使思路清晰明了,最终使问题的解决明朗化;把握这种思想,不管是空间线线距离,线面距离,面面距离问题,一般我们都能转化成点线或点面距离,再借助平面法向量很好地解决了.)

(1)分析:要证平面EFG平面ACB1,由题设知只要证BD1垂直平面ACB1即可.
证明:以D为坐标原点,建立空间直角坐标系,如图5,不妨设正方体棱长为a,则A(a,0,0),B(a,a,0),C(0,a,0),D1(0,0,a),B1(a,a,a),E(xE,0,a),F(0,yF,a),G(0,0,zG).
∴
 =(-a,-a,a),
=(-a,-a,a),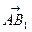 =(0,a,a),
=(0,a,a),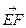 (-xE,yF,0),
(-xE,yF,0),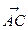 =(-a,a,0),
=(-a,a,0),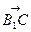 =(-a,0,-a),
=(-a,0,-a),∵
 ·
·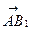 =(-a,-a,a)·(0,a,a)=0,
=(-a,-a,a)·(0,a,a)=0,∴
 ⊥
⊥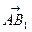 ,
,同理
 ⊥
⊥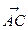 ,
,而
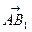 与
与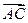 不共线且相交于点A,
不共线且相交于点A,∴
 ⊥平面ACB1,又已知
⊥平面ACB1,又已知 ⊥平面EFG,
⊥平面EFG,∴平面EFG∥平面ACB1;
又因为
 ⊥平面EFG,所以
⊥平面EFG,所以 ⊥
⊥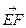 ,
,则
 ·
·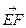 =0,
=0, 即 (-a,-a,a)·(-xE,yF,0)=0,
化简得 xE-yF=0;
同理 xE-zG="0, " yF-zG=0,
易得
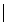
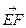
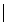 =
=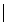
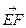
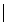 =
=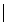
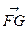
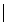 ,
,∴ △EFG为正三角形.
(2)解:因为△EFG是正三角形,显然当△EFG与△A1C1D重合时,△EFG的边最长,其面积也最大,此时,
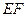 =A1C1=
=A1C1=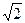 ·a,
·a,∴
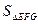 =
=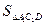
=
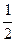
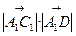 ·sin600
·sin600=
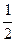 (
(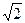 ·a)2·
·a)2·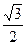
=
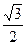 ·a2 .
·a2 .此时EF与B1C的距离即为A1C1与B1C的距离,由于两异面直线所在平面平行,所求距离转化为求点B1到平面A1C1D的距离,记A1C1与B1D1交于点O1,作O1H∥D1B并交BB1于点H,则O1H⊥平面A1C1D,垂足为O1,则O1(
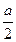 ,
,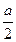 ,a),H(a,a,
,a),H(a,a,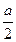 ),而
),而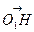 作为平面A1C1D的法向量,
作为平面A1C1D的法向量,所以异面直线EF与B1C的距离设为d是
d =
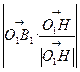 =
=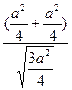 =
=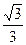 ·a.
·a.(证明(2)时一般要找到求这两平面距离的两点,如图5*,而这两点为K与J,在立体图形中较难确定,且较难想到通过作辅助线DO1,OB1来得到,加上在如此复杂的空间图形中容易思维混乱,但只要借助平面法向量求线段的射影长度的思想,结合题设,使思路清晰明了,最终使问题的解决明朗化;把握这种思想,不管是空间线线距离,线面距离,面面距离问题,一般我们都能转化成点线或点面距离,再借助平面法向量很好地解决了.)

练习册系列答案
相关题目
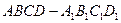 的棱长为
的棱长为 ,
,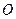 是
是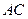 与
与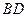 的交点,
的交点,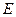 是
是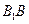 上一点,且
上一点,且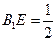 .(Ⅰ)求证:
.(Ⅰ)求证: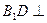 平面
平面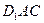 ;
;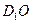 与
与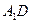 所成角的余弦值;
所成角的余弦值;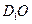 与平面
与平面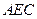 所成角的正弦值.
所成角的正弦值.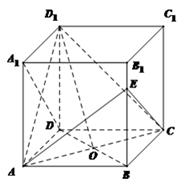
 的侧棱与底面垂直,
的侧棱与底面垂直, ,MN分别是
,MN分别是 的中点,P点在
的中点,P点在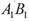 上,且满足
上,且满足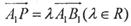
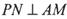
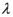 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角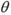 最大?并求出该最大角的正切值;
最大?并求出该最大角的正切值;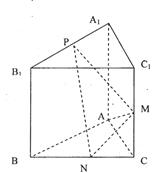
 三点不共线,
三点不共线, 为平面
为平面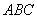 外任一点,若由
外任一点,若由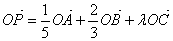 确定的一点
确定的一点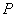 与三点
与三点 .
.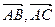 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S; 分别与向量
分别与向量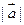 =
=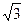 ,求向量
,求向量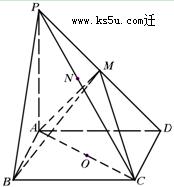
 的长方体被截面
的长方体被截面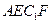 所截面而得到的,其中
所截面而得到的,其中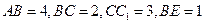 .
.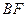 的长;
的长;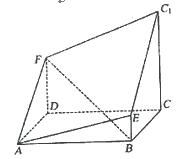
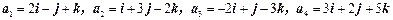 ,试问是否存在实数
,试问是否存在实数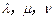 ,使
,使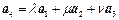 成立?如果存在,求出
成立?如果存在,求出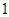 的正方体
的正方体 中,
中,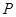 为线段
为线段 上的动点,则下列结论错误的是
上的动点,则下列结论错误的是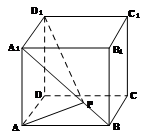
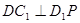
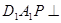 平面
平面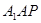
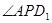 的最大值为
的最大值为
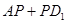 的最小值为
的最小值为