题目内容
1.求下列不等式的解集:(1)|2x-1|≥3;
(2)|2x-1|≤5;
(3)3≤|2x-1|≤5.
分析 (1)不等式|2x-1|≥3等价为:2x-1≥3或2x-1≤-3;
(2)不等式|2x-1|≤5等价为:-5≤2x-1≤5;
(3)不等式3≤|2x-1|≤5等价为:-5≤2x-1≤-3或3≤2x-1≤5.
解答 解:(1)不等式|2x-1|≥3等价为:
2x-1≥3或2x-1≤-3,
解得,x≥2或x≤-1,
因此,该不等式的解集为(-∞,-1]∪[2,+∞);
(2)不等式|2x-1|≤5等价为:
-5≤2x-1≤5,
解得,-2≤x≤3,
因此,该不等式的解集为[-2,3];
(3)不等式3≤|2x-1|≤5等价为:
-5≤2x-1≤-3或3≤2x-1≤5,
解得,-2≤x≤-1或2≤x≤3,
因此,该不等式的解集为[-2,-1]∪[2,3].
点评 本题主要考查了绝对值不等式的解法,合理等价与转化是解不等式的关键,属于基础题.

练习册系列答案
相关题目
9.$\frac{1}{2}$-sin215°的值是( )
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
16.关于x的方程x2-2x+lg(2a2-a)=0有一个正根和一个负根的充分不必要条件是( )
| A. | -$\frac{1}{2}$<a<1 | B. | -$\frac{1}{2}$<a<0 | C. | 0<a<1 | D. | -$\frac{1}{2}$<a<0或$\frac{1}{2}$<a<1 |
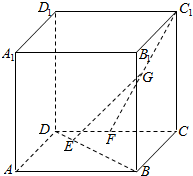 如图,已知正方体ABCD-A1B1C1D1的棱长为4,点E在线段BD上且|DE|=$\frac{1}{3}$|EB|,点F是CD的中点,G为C1F的中点,求EG的长.
如图,已知正方体ABCD-A1B1C1D1的棱长为4,点E在线段BD上且|DE|=$\frac{1}{3}$|EB|,点F是CD的中点,G为C1F的中点,求EG的长.