题目内容
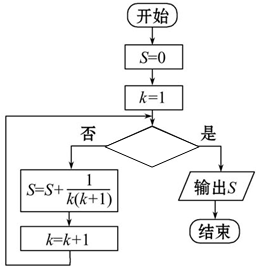 已知算法框图如下:
已知算法框图如下:(1)若算法计算
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 99×100 |
(2)若菱形框(条件框)处的条件为“k≥2014”,则输出的结果为多少?
考点:程序框图
专题:算法和程序框图
分析:(1)根据算法的功能确定跳出循环的k值为100,可得判断框的条件是k≥100或k>99;
(2)根据判断框的条件确定跳出循环的k值为2014,再利用裂项相消法求出输出S的值.
(2)根据判断框的条件确定跳出循环的k值为2014,再利用裂项相消法求出输出S的值.
解答:
解:(1)由算法的功能是计算
+
+
+…+
的值,
∴跳出循环的k值为100,∴判断框的条件是k≥100或k>99;
(2)若菱形框(条件框)处的条件为“k≥2014”,则跳出循环的k值为2014,
∴输出S=
+
+
+…+
=1-
+
-
+…+
-
=1-
=
,
∴输出的结果为
.
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 99×100 |
∴跳出循环的k值为100,∴判断框的条件是k≥100或k>99;
(2)若菱形框(条件框)处的条件为“k≥2014”,则跳出循环的k值为2014,
∴输出S=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2013×2014 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2013 |
| 1 |
| 2014 |
| 1 |
| 2014 |
| 2013 |
| 2014 |
∴输出的结果为
| 2013 |
| 2014 |
点评:本题考查了循环结构的程序框图,本题是程序框图的典型题目,根据算法的功能判定跳出循环的k值是关键.

练习册系列答案
相关题目
若复数zl=-1+2i,z2=-1-i,其中i是虚数单位,则(zl+z2)i的虚部为( )
| A、-2i | B、-2 | C、2i | D、2 |