题目内容
若复数zl=-1+2i，z2=-1-i，其中i是虚数单位，则（zl+z2）i的虚部为（ ）
| A、-2i | B、-2 | C、2i | D、2 |
考点：复数代数形式的混合运算
专题：数系的扩充和复数
分析：根据复数的四则运算先化简复数，即可得到结论．
解答：
解：∵复数zl=-1+2i，z2=-1-i，
∴（zl+z2）i=（-2+i）i=-2i+i2=-1-2i，
故（zl+z2）i的虚部为-2，
故选：B
∴（zl+z2）i=（-2+i）i=-2i+i2=-1-2i，
故（zl+z2）i的虚部为-2，
故选：B
点评：本题主要考查复数的有关概念，利用复数的四则运算先进行化简是解决本题的关键，比较基础．
练习册系列答案
相关题目
已知函数f（x）=
sinx+
cosx在x0处取得最大值，则x0可能是（ ）
| ||
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
“k=-1”是“两直线kx+3y-2=0和（2-k）x+y-7=0互相垂直”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
已知角α的终边过点P（x，-3）且cosα=-
，则x的值为（ ）
| ||
| 2 |
A、±3
| ||||
B、3
| ||||
C、-3
| ||||
D、-
|
数学协会是我们学校的一个研究型社团，深受同学们的喜爱，在2013年9月27、28日下午的社团招新活动中，较多的同学加入了数学协会．设命题p是“甲同学加入了数学协会”，命题q是“乙同学加入了数学协会”，则命题“甲、乙至少有一位同学没有加入数学协会”可表示为（ ）
| A、￢p∨￢q | B、p∨q |
| C、p∨￢q | D、￢p∧￢q |
已知△ABC中，tanA=-
，那么cosA等于（ ）
| 5 |
| 12 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
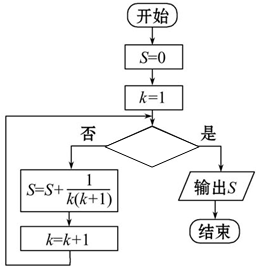已知算法框图如下：