题目内容
在△ABC中，若
+
=2，且△ABC的周长为12．
（1）求证：△ABC为直角三角形；
（2）求△ABC面积的最大值．
| cosA |
| sinB |
| cosB |
| sinA |
（1）求证：△ABC为直角三角形；
（2）求△ABC面积的最大值．
考点：解三角形,正弦定理,余弦定理
专题：解三角形
分析：（1）通过已知条件，化简表达式，讨论sinA＞cosB与sinA＜cosB，方程不成立推出sinA=cosB，然后证明△ABC为直角三角形；
（2）设直角三角形的两直角边为a、b，斜边为c，因为L=a+b+c，c=
，两次运用均值不等式即可求解△ABC面积的最大值．
（2）设直角三角形的两直角边为a、b，斜边为c，因为L=a+b+c，c=
| a2+b2 |
解答：
解：（1）在△ABC中sinA＞0，sinB＞0，
∵
+
=2，
∴sinAcosA+cosBsinB=2sinBsinA，
可得sinAcosA-sinBsinA=sinBsinA-cosBsinB
可得sinA（cosA-sinB）=sinB（sinA-cosB），…①．
∵A、B、C是三角形内角，由①可得若sinA＞cosB，则cosA＞sinB，
若sinA＜cosB，则cosA＜sinB，这都是不可能的，
∴sinA=cosB，cosA=sinB，可得A=B=45°，∴C=90°，
∴△ABC是直角三角形．
（也可以sinA=sin（90°-B），∴A+B=90°，∴C=90°，∴△ABC是直角三角形．）
（2）设直角三角形的两直角边分别为a、b，斜边为c，则直角三角形的面积S=
ab．
由已知，得a+b+c=12，∴a+b+
=12，
∴12=a+b+
≥2
+
=（2+
）
，
∴
≤
=12-6
，∴ab≤（12-6
）2=216-132
，
∴S=
ab≤108-66
，当且仅当a=b=12-6
时，S取最大值．
∵
| cosA |
| sinB |
| cosB |
| sinA |
∴sinAcosA+cosBsinB=2sinBsinA，
可得sinAcosA-sinBsinA=sinBsinA-cosBsinB
可得sinA（cosA-sinB）=sinB（sinA-cosB），…①．
∵A、B、C是三角形内角，由①可得若sinA＞cosB，则cosA＞sinB，
若sinA＜cosB，则cosA＜sinB，这都是不可能的，
∴sinA=cosB，cosA=sinB，可得A=B=45°，∴C=90°，
∴△ABC是直角三角形．
（也可以sinA=sin（90°-B），∴A+B=90°，∴C=90°，∴△ABC是直角三角形．）
（2）设直角三角形的两直角边分别为a、b，斜边为c，则直角三角形的面积S=
| 1 |
| 2 |
由已知，得a+b+c=12，∴a+b+
| a2+b2 |
∴12=a+b+
| a2+b2 |
| ab |
| 2ab |
| 2 |
| ab |
∴
| ab |
| 12 | ||
2+
|
| 2 |
| 2 |
| 2 |
∴S=
| 1 |
| 2 |
| 2 |
| 2 |
点评：本题考查解三角形，分类讨论思想的应用，利用均值不等式解决实际问题时，列出有关量的函数关系式或方程式是均值不等式求解或转化的关键．
练习册系列答案
阅读快车系列答案
相关题目
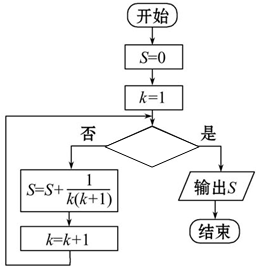已知算法框图如下：